9709/41/M/J/25q6 (although part b requires knowledge of “work done” and “energy” from the next section) – Mark Scheme
Two particles, P and Q, of masses 0.3kg and 0.6kg respectively, are attached to the ends of a light inextensible string. The string passes over a smooth pulley fixed at a point B where the inclined planes AB and BC meet. P lies on the smooth plane AB which is inclined at an angle 
(a) It is given that the plane BC is smooth. Find the tension in the string and the acceleration of Q. [5 marks]
(b) It is given instead that the plane BC is rough. The work done against the frictional force when Q moves 2m down the plane is 1.8J. You should assume that P does not reach the pulley and that Q does not reach C.
Use an energy method to find the speed of Q when it has moved 2m down the plane. [4 marks]
9709/42/M/J/25q5 – Mark Scheme
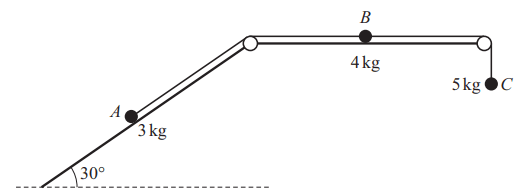
One end of a light inextensible string is attached to a particle A of mass 3kg. The other end of the string is attached to a particle B of mass 4kg. Particle A is in contact with a rough plane inclined at 
Both strings are taut and pass over small smooth pulleys that are fixed at the ends of the horizontal plane. The part of the string from A to the pulley is parallel to a line of greatest slope of the inclined plane, and A, B and C are in the same vertical plane (see diagram).
The system is released from rest. In the subsequent motion, C moves vertically downwards with acceleration 2ms-2, and neither A nor B reach a pulley.
(a) Find the tensions in each of the strings. [3 marks]
(b) Find the coefficient of friction between A and the inclined plane. [4 marks]
When the system has been in motion for 1.5s, the string attached to A breaks.
(c) Find the total distance that A travels up the plane from the instant that the system is released from rest to the instant that A comes to instantaneous rest. [5 marks]
9709/43/M/J/25q2 – Mark Scheme
A van of mass 4500kg is towing a trailer of mass 350kg along a straight horizontal road. The van and trailer are connected by a light rigid tow-bar which is parallel to the road. There are resistance forces of X N on the van and 120 N on the trailer. The driving force produced by the van’s engine is 2500 N. The tension in the tow-bar is T N, and the acceleration of the van is 0.4ms-2.
Find the value of X and the value of T. [4 marks]
9709/43/M/J/25q4 – Mark Scheme
Three blocks P, Q and R, of masses 25kg, 20kg and m kg respectively, are held in equilibrium by three light inextensible strings OP, OQ and OR. The strings OP and OR both pass over small fixed smooth pulleys A and B respectively, with P and R hanging vertically below the pulleys. The block Q hangs vertically below the point O. The angle between OA and the vertical is 
Find the value of m and the value of 
9709/42/F/M/25q4 – Mark Scheme
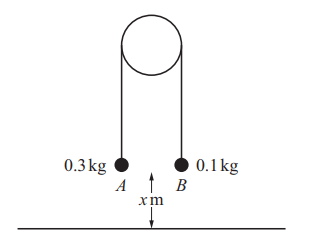
Two particles A and B have masses 0.3kg and 0.2kg respectively. The particles are attached to the end of a light inextensible string. The string passes over a fixed smooth pulley, and the particles hang vertically below the pulley. Both particles are initially at a height of xm above horizontal ground (see diagram). The system is released from rest.
(a) Find the tension in the string and the acceleration of the particles. [4 marks}
During the subsequent motion, B does not reach the pulley. When A reaches the ground, it comes to rest.
(b) Given that the greatest height of B above the ground is 1.2m, find the value of x. [3 marks]
9709/41/O/N/24q1 – Mark Scheme
Two particles, of masses 1.8kg and 1.2kg, are connected by a light inextensible string that passes over a fixed smooth pulley. The particles hang vertically. The system is released from rest.
Find the magnitude of the acceleration of the particles and find the tension in the string. [4 marks]
Maths with David 