9231M. Motion of a Projectile

Section 1: Finding the horizontal distance travelled by particles

We consider projectiles moving under the force due to gravity. We consider the horizontal and vertical components of their displacement, velocity and acceleration using the SUVAT formulae (as if only gravity is acting on them they have constant acceleration).

In our models we typically:

ignore air resistance;
treat projectiles as particles;
ignore any rotational forces; and
assume that the force due to gravity is constant.

A projectile travels on a parabolic trajectory.

We already know that the displacement of a projectile is always $s = ut + \frac{1}{2} at^2$ , which is a quadratic function (graphically represented by a parabola).

If we imagine a particle projected at angle 𝜽 (anticlockwise from horizontal) with velocity u, we can resolve its initial velocity into horizontal and vertical directions as ucos𝜽 and usin𝜽.

So, using the SUVAT equation v = u + at, as the only acceleration acting on the particle is downwards due to gravity, we have horizontal velocity of v_X=ucos𝜽 and vertical velocity of v_Y=usin𝜽 – gt.

At the vertex of the particle’s parabolic path, i.e. at its maximum height, v_Y=0, so from the above, $t = \frac{u sin \theta}{g}$

If the particle is projected from the ground, from symmetry we can see that the time it takes to travel to the top of its path is equal to the time it takes to return to the ground, so we can conclude that the total flight time is $t = \frac{2u sin \theta}{g}$ .

Considering displacement, we have $s_X = ucos \theta t$ and $s_Y = usin \theta t + \frac{1}{2} at^2$

If we substitute the time of the flight path from projection to returning to the ground into s_X above, we get $s_X = ucos \theta \times \frac{2u sin \theta}{g}$ , or $s_X = \frac{u^2 2cos \theta sin \theta}{g}$ . We can use trigonometric double angle formulae to write this as $s_X = \frac{u^2 sin 2 \theta}{g}$ . This is the range of the the projectile, its maximum horizontal difference.

We can see that when 𝜽 = 45°, so sin2𝜽 = 1 and the range is maximised. So an angle of elevation of 45° achieves maximum displacement.

Worked Example 1

A particle is projected from a point on a horizontal surface with initial speed 20ms^-1 at an angle of elevation of 25°. Find:

the range of the particle;
the time taken to reach the highest point; and
the speed of the particle when t = 0.5.

A particle may be projected from a point above the ground (like when a tennis ball is hit). If we wish to find the velocity when the particle hits the ground, we can simply use the SUVAT formula v² = u²+2as in the vertical direction, with the s indicating how far above the ground it is projected from and the above formula v_X=ucos𝜽 in the horizontal direction, using Pytahgoras theorem with these two results to find the velocity when it hits the ground.

Worked Example 2

A particle is projected from the top of a platform 15m above the horizontal floor below. The angle of projection is 45° and the initial speed is 25ms^-1. Find:

the exact time taken to reach the horizontal floor below; and
the exact speed of the particle as it hits the floor.

Projectiles can also be launched at an angle below the horizontal (an angle of depression), i.e pointing partly downwards. If we wish to find how far such a particle travels horizontally, we first must find how long it takes to reach the ground and then use this time value to calculate its horizontal displacement.

We solve the quadratic equation $s = ut + \frac{1}{2} at^2$ downwards, taking acceleration as positive and then substitute the positive result for t into $s_X = utcos \theta$

Worked Example 3

An aircraft is flying over the ocean to collect data. It is travelling horizontally at a speed of 50ms^-1 when it launches a sensor at an angle of 25° below the horizontal with an initial speed of 10ms^-1. Given that the plane is 1km above the ocean, and assuming that the ocean surface is flat and that air resistance is negligible, find the speed of the sensor when it is 100m from the surface of the ocean.

Exercise 1

A projectile is launched from point O on horizontal ground, landing at the point A.
- OA = 205m, $\theta = 40 ^{\circ}$ . Find the speed u.
- $\theta = 30 ^{\circ}$ , u = 32ms^-1. Find the range OA.
- OA = 130m, u = 40ms^-1. Find the possible angles of projection $\theta$ .
A projectile is launched from a point on horizontal ground with speed U. Given that the horizontal distance travelled before hitting the ground again is 140m and that the angle of projection is 25° above the horizontal, find U.
In a game a ball is kicked from the point O on horizontal ground, so that it lands on a scoring area which extends from 20m to 25m from O. If the angle of elevation when kicked is 35°, within what interval must the initial speed be to ensure that the ball lands in the scoring area.
A particle is projected from point A on horizontal ground with initial speed 25ms^-1 and angle of elevation $\theta$ . Given that the range of the particle is 60m, find the value of the angle $\theta$ .
A football player kicks a football from a point on the ground with an angle of elevation of 15°. The ball must land on horizontal ground level between 10m and 20m from the player’s feet. Find the possible range of values of the initial speed of the football.
A basketball is thrown with speed 10ms^-1 from a point 2m above the ground, at an angle of 45° above the horizontal. Find the speed of the basketball when it is at a height of 4m for the second time during its motion.
A particle of mass 2kg is fired up a smooth slope of length 4m, with initial speed 10ms^-1, which is inclined at 30° above the horizontal. The bottom of the slope is at the same level as horizontal ground.
- Find the speed of the particle at the top of the slope.
- The particle now flies off the slope and travels as a projectile. Find the greatest height achieved above the ground level.
A particle is projected horizontally from a point that is 12m above a horizontal surface, with a speed of 15ms^-1. Find the horizontal distance travelled before the particle hits the surface below.
A particle is projected across a horizontal area of land, with initial speed 30 ms^-1 and inclined at an angle of 40°. Find the duration of time for which the particle is at least 10m above the ground.
A small stone is thrown from the top of a building that is 30m tall. The stone is given an initial speed of 5ms^-1 and is directed downwards with an angle of depression of 15°
- Find the time taken for the stone to reach the ground.
- Find the speed of the stone as it hits the ground.

Answers

Projectiles Exercise 1 Worked Solutions

Section 2: Cartesian equation of trajectory

We saw above that a particle’s initial speed and angle of projection determines its general motion. We found that the horizontal distance travelled at time t is $x = utcos \theta$ , which can be rewritten as $t = \frac{x}{ucos \theta}$

We also found that the vertical distance travelled at time t is $y = utsin \theta - \frac{1}{2} gt^2$ . If we substitute the above expression for t into this, we get: $y = u(\frac{x}{ucos \theta})sin \theta - \frac{1}{2} g(\frac{x}{ucos \theta})^2$ , so, our Cartesian equation of the trajectory of a projectile is: $y = xtan \theta - \frac{gx^2}{2u^2}sec^2 \theta$

This is a quadratic equation, with a negative coefficient for x², so represents a parabola opening downwards.

We can use this equation to find horizontal distance travelled (spoiler alert: it gives the same result as we got in the section above):

When a projectile returns to the ground, y = 0, so $0 = xtan \theta - \frac{gx^2}{2u^2}sec^2 \theta$ , so $x(tan \theta - \frac{g}{2u^2}xsec^2 \theta)=0$ , so the start and finish points of the motion are x=0 and $x = \frac{u^2sin2 \theta}{g}$

Worked Example 1

A projectile is launched from a point O, 1m above the horizontal ground level. It has initial speed of 20ms^-1 and angle of elevation of 25°. Find the horizontal distance from O when the particle is 2m above the ground and descending.

If we consider downward projection, the only difference is that gravity is now effectively positive, so we have $y = xtan \theta + \frac{gx^2}{2u^2}sec^2 \theta$

Worked Example 2

A ball is thrown from the top of a building of height 20m. The ball is thrown such that the initial speed is U ms^-1 and the angle of depression of the throw is 30°. Find:

(a) the horizontal distance travelled in terms of U; and

(b) the horizontal distance when U = 5.

Worked Example 3

A projectile follows the path y=0.3x – 0.1x². Find the initial speed and the angle of elevation of the particle.

Let’s focus on the direction of motion of a particle at various points along its path. Note that the horizontal component of velocity remains unchanged throughout its motion and that the vertical component of velocity starts with its greatest positive value, reduces to zero by the highest point of its trajectory and then reaches its greatest negative value when it reaches the ground again.

We can calculate the height of a particle at a point on its path if we know the direction it is facing at that point, by relating the horizontal and the vertical components of its velocity at that point and using that relationship with the general equations for the horizontal and vertical components of velocity to calculate the time at which that occurs. Once we know the time, we can plug that into $y = utsin \theta - \frac{1}{2}gt^2$ to find the height of the particle when it is travelling in that direction.

Worked Example 4

A particle is projected from the top of a tower that is 50m tall. Its initial speed is 25ms^-1 at angle of depression 10°. Find the height of the particle above the ground when the downward angle of the direction of the particle is 30°.

Exercise 2

A particle is projected from horizontal ground with initial speed 15ms^-1 and angle of elevation 60º. Find the horizontal distance traveled when the particle is first a height of 8m above ground level.
A ball is thrown from a point of 2m above horizontal ground. The initial speed is 20ms^-1 and the angle of elevation is 45º. Find the horizontal distance covered when the ball is 12m above the ground.
A particle is projected from ground level with initial speed 30ms^-1 at an angle of elevation of 25º. Find the horizontal distance traveled from the starting point when the height is 4m for the first time.
A particle is projected from a point 5m above a horizontal plane. The angle of elevation is 10º. Given that the particle travels 75m before hitting the ground, find the initial speed.
A particle is projected from a point 4m above horizontal ground, with an initial speed of 20ms^-1 and an angle of elevation of 20º. Find the direction of the particle as it lands on the ground.
A ball is kicked at a house window. The window is 4m up a vertical wall from a horizontal floor. The ball is kicked from a position that is 12m distance from the foot of the wall. If the ball enters the window at an angle that is 30º below the horizontal, find:
- the time taken to reach the window;
- the initial speed of the ball.
A particle is projected from the top of an office building that is 35m tall. The initial speed is 14ms^-1 and the angle of depression is 20º. Find the height of the particle above the ground when the downward angle of the direction of the particle is 45º.
A particle is projected from a point on a horizontal surface with initial speed u and angle of elevation β. At any time during its motion, the particle is at the position (x,y), where x is the horizontal distance traveled and y is the vertical distance traveled. Show that $y = xtan \beta - \frac{gx^2}{2u^2}(1 + tan^2 \beta)$ .
A particle is projected from a point on a horizontal plane with speed 20ms^-1 at an angle of elevation of 𝜽. Given that the particle passes through the point x=20, y=10, find the possible angles of elevation.
A particle is projected from a point on horizontal ground with initial speed u and angle of elevation a. Show that x² + y² = u²t² – 10yt² – 25t⁴, where (x,y) is the particle’s position at time t.

Answers to Exercise 2

Projectiles Exercise 2 Worked Solutions

Mixed Exercise

Answers to Mixed Exercise

(i) Proof, (ii) 38.4m, 17.8m, (iii) See image below

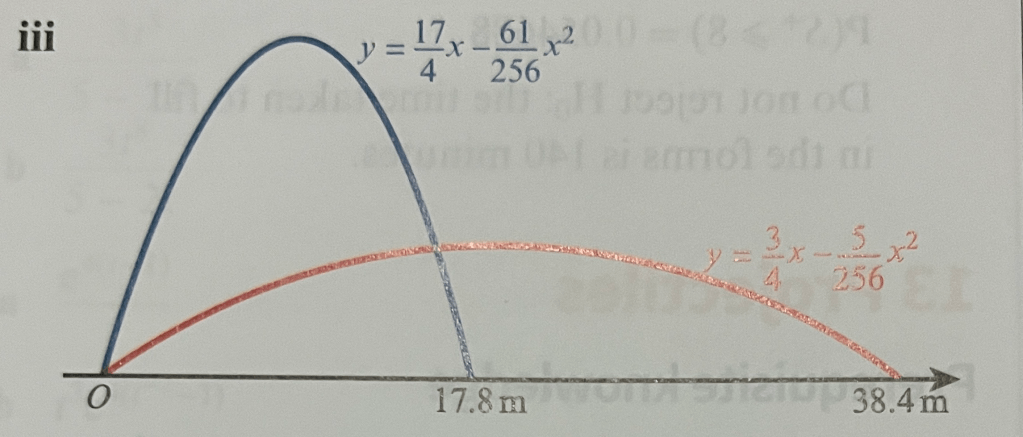
2. (i) $y = x - \frac{1}{10}x^2$ , (ii) x = 4.23, (iii) 𝜽 = 8.8°

3. (i) k = 1/2, 2, proof, (ii) t = 0.894s (iii) 16.3ms^-1, 15.9 above horizontal

Projectiles Mixed Exercise Worked Solutions

Worked Exam Style Question

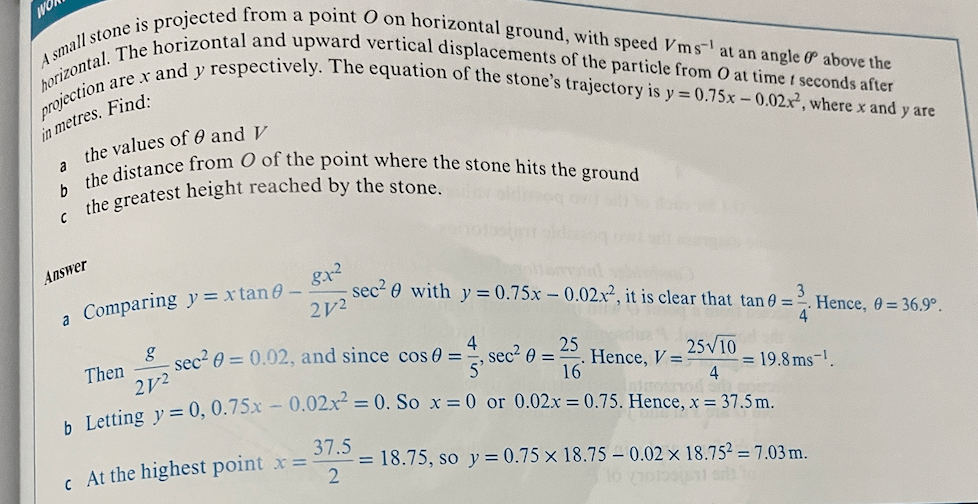
Relevant Past Exam Paper Questions

Summer 2023 paper 31 q7

At time t seconds, a particle P is projected with speed $40ms^{-1}$ at an angle $\theta$ above the horizontal from a point O on a horizontal plane and moves freely under gravity. The greatest height achieved by P during its flight is H metres and the corresponding time is T seconds.

(a) Obtain expressions for H and T in terms of $\theta$ . [2 marks]

During the time between t=T and t=3, P descends a distance of $\frac{1}{4} H$

(b) Find the value of $\theta$ [4 marks]

Summer 2023 paper 33 q7a (only part a is relevant as part b requires momentum)

The points O and P are on a horizontal plane, a distance 8m apart. A ball is thrown from O with speed $u ms^{-1}$ at an angle $\theta$ above the horizontal, where $tan \theta = \frac{4}{3}$ . At the same instant, a model aircraft is launched with speed $5 ms^{-1}$ parallel to the horizontal plane from a point 4m vertically above P. The model aircraft moves in the same vertical plane as the ball and in the same horizontal direction as the ball. The model aircraft moves horizontally with a constant speed of $5 ms^{-1}$ . After T s, the ball and the model aircraft collide.

(a) Find the value of T [6 marks]

Winter 2022 paper 31 q7 (only part a is relevant as part b requires momentum)

A particle P is projected with speed $Vms^{-1}$ at an angle of 75º above the horizontal from a point O on a horizontal plane. It then moves freely under gravity.

(a) Show that the total time of flight, in seconds, is $\frac{2V}{g} sin75^{\circ}$ [2 marks]

Winter 2022 paper 32 q5

A particle P is projected with speed $ums^{-1}$ at an angle of $\theta$ above the horizontal from a point O on a horizontal plane and moves freely under gravity. The horizontal and vertical displacements of P from O at a subsequent time t s are denoted by x m and y m respectively.

(a) Show that the equation of the trajectory is given by $y = tan \theta - \frac{gx^2}{2u^2} (1+tan \theta )$ . [4 marks]

In the subsequent motion P passes through the point with coordinates (30,20).

(b) Given that one possible value of $tan \theta$ is $\frac{4}{3}$ , find the other possible value of $tan \theta$ [5 marks]

Summer 2022 paper 32 q7

Particles P and Q are projected in the same vertical plane from a point O at the top of a cliff. The height of the cliff exceeds 50m. Both particles move freely under gravity. Particle P is projected with speed $\frac{35}{2} ms^{-1}$ at an angle $\alpha$ above the horizontal, where $tan \alpha = \frac{4}{3}$ . Particle Q is projected with speed $u ms^{-1}$ at an angle $\beta$ above the horizontal, where $tan \beta = \frac{1}{2}$ . Particle Q is projected one second after the projection of particle P. The particles collide T seconds after the projection of particle Q.

(a) Write down expressions, in terms of T, for the horizontal displacements of P and Q from O when they collide and hence show that $4uT = 21 \sqrt{5} (T+1)$ [4 marks]

(b) Find the value of T [4 marks]

Summer 2022 paper 33 q3

A particle P is projected with speed $25 ms^{-1}$ at an angle $\theta$ above the horizontal from a point O on a horizontal plane and moves freely under gravity. After 2s the speed of P is $15 ms^{-1}$

(a) Find the value of $sin \theta$ [5 marks]

(b) Find the range of the flight [3 marks]

Winter 2021 paper 31 q5

A particle P is projected from a point O on a horizontal plane and moves freely under gravity. Its initial speed is $u ms^{-1}$ and its angle of projection is $sin^{-1}(\frac{4}{5})$ above the horizontal. At time 8s after projection, P is at the point A. At time 32s after projection, P is at the point B. The direction of motion of P at B is perpendicular to its direction of motion at A.F

Find the value of u. [7 marks]

9231M. Motion of a Projectile

Share this: