9231. Mechanics. Hooke’s Law

So far we have always called strings inextensible, a modelling simplification that ignores their elasticity, i.e. how much they can be stretched out when they are under tension. The force required to stretch a string or spring is directly proportional to its extension (i.e. how much it lengthens).

Throughout this section we will use the following naming convention:

The letter l will be used for the natural length (i.e. unextended length) of a spring;

The letter x will be used for the length is is extended by.

𝞴 will be used for the modulus of elasticity, which is measured in Newtons.

Hooke’s Law

As the force required to stretch a string is directly proportional to the length by which the string is extended, we can write T= kx.

The constant of proportionality k varies between different materials and also dependes on the natural length of the string. Hence we replace k with 𝞴/l, where 𝞴, the modulus of elasticity depends on the specific material.

So we write Hooke’s law as $T = \frac{ \lambda x}{l}$

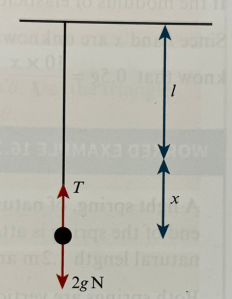
Suppose we have a light, elastic string with length 1m, with one end attached to the ceiling and the other end attached to a 2kg particle.

If the system starts at rest and the string has modulus of elasticity 50N, we will find the length of the extended string.

First we resolve vertically, i.e. T = 2g.

Then, using Hooke’s Law, $\frac{ \lambda x }{l} = 2g$ .

Substituting in the given values gives: $\frac{50 \times x}{1}=2g$ , so x = 0.4m.

The length of the extended spring is therefore 1 + 0.4 = 1.4m.

Worked Example 1

A block of 3kg is attached to one end of a light, elastic string of natural length 2m. The other end of the string is attached to a ceiling, and the string and block are at rest in equilibrium. Given that the extension in the string is 0.8m, find the value of 𝞴.

Elastic springs

As well as strings, we can have springs. These can be extended, but they can also be compressed.

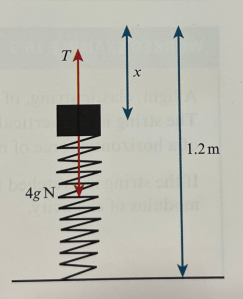
We consider a light spring with natural length 1.2m fixed to a horizontal floor and standing vertically.

A 4kg mass is placed on top of the spring so that the spring compresses by distance x. The modulus of elasticity is 45N.

So the spring will be in thrust instead of tension as it resists compression. We can calculate x using Hooke’s Law, as $4g = \frac{45 \times x}{1.2}$ , so x = 1.07m

Now let’s consider stretching a spring of unknown natural length, fixed to a ceiling at one end and with a 0.5kg mass attached to the other end. The spring hangs in equilibrium such that the length of the spring is now 12cm. We know that the modulus of elasticity is 10N and want to find the natural length of the spring.

As l and x are unknown, we first write l + x = 0.12.

Hooke’s Law tells us that $0.5g = \frac{10 \times x}{l}$ , so x = 0.5l, and so 1.5l = 0.12, giving l = 0.08m

Worked Example 2

A light spring, of natural length 1.6m and modulus of elasticity 40N, is attached to the floor at point A. The other end of the spring is attached to a block, C, of mass 2kg. The same block is attached to a second light spring, or natural length 1.2m and modulus of elasticity 25N, which is then attached to a ceiling at point B.

Both springs are vertical. A and C are vertically below B.

If AB is 4.5m, find the distance AC.

Worked Example 3

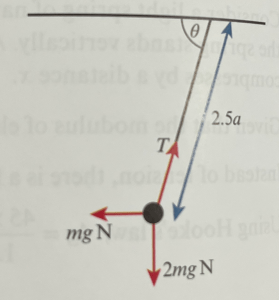
A light, elastic string, of natural length 2a, has a mass of 2m attached to one end. The string is in a vertical plane and the system rests in equilibrium with the aid of a horizontal force of magnitude mg.

If the string is stretched to a length of 2.5a, find the tension in the string and the modulus of elasticity.

Worked Example 4

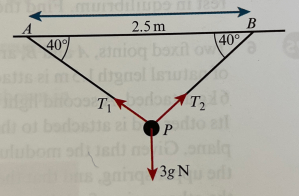
A light, elastic string of natural length 1.5m is stretched between points A and B that are 2.5m apart (in a horizontal line). A particle, P, of mass 3kg, is attached to the midpoint of the string. The string rests in equilibrium with the parts of the string making an angle of 40° to the horizontal, as shown in the diagram above.

Find the value of the modulus of elasticity.

Exercise 1

A light elastic string of natural length l and modulus of elasticity 𝞴 is stretched by a force T, causing the string to extend. In each of the following cases, work out the unknown value:
- T = 15N, 𝞴 = 40N, l = 1.2m. Find the extension;
- T = 25N, l = 1.5m, x = 0.5m. Find the modulus of elasticity;
- T = (3𝞴 – 11)N, l = 2m, x = 0.5m. Find the tension in the string.
A light string of unknown natural length is fixed to a ceiling at one end, with a mass of 0.4kg attached to the other end. The string is allowed to hang in equilibrium such that the length of the string is now 15cm. If the modulus of elasticity is 20N, find the natural length of the string.
A light string is attached to a ceiling at the point A. The natural length of the string is 1.3m and the string has a mass of 3m attached to the free end. The string is allowed to rest in equilibrium. Given that the string is stretched by an extra 20% in length, find the value of the modulus of elasticity.
A light, elastic string is attached to a ceiling at the point A. The natural length of the string is 1.6m and the string has a mass of 2m attached to the other end. The string is allowed to rest in equilibrium. Given that the string is stretched by 40% of its length, find the value of the modulus of elasticity.
Two points, A and B, lie 3m apart on a smooth horizontal surface. A light, elastic string, of natural length 0.8m and modulus of elasticity 70N, is attached to A. Its other end is attached to a particle, P, of mass m. A second light, elastic string, of natural length 1.3m and modulus of elasticity 50N, is attached to the point B. Its other end is also attached to the particle P. The particle is allowed to rest in equilibrium. Find the distance BP.
Two fixed points, A and B, are such that A is 4m vertically above B. A light spring of natural length 1.5m is attached to A, and at the other end it has a particle of mass 6kg attached. A second light spring of natural length 1m is attached to the point B. Its other end is attached to the same particle. Both springs are in the same vertical plane. Given that the modulus of elasticity of the lower spring is one third of that of the upper spring, and that the extension of one spring is six times the compression of the other spring, find the modulus of elasticity of the lower spring.
A particle, P, of mass 3.5kg is attached to one end of a light, elastic string, of natural length 1.2m. The other end of the string is attached to a fixed point, O. The particle is allowed to rest in equilibrium with P 1.8m below O.
- Show that the modulus of elasticity 𝞴 is 7g N;
- The particle is now pulled horizontally to the side by a force of magnitude X N so that the angle between the string and the downward vertical is 60º. Given that the particle is at the same vertical level as it was before, find the value of X.
A particle, P, of mass 4kg is resting on a rough, horizontal table. A light, elastic string, of natural length 2m and modulus of elasticity 50N, is attached to P. It is then passed over a smooth pulley to a second particle, Q, of mass 3kg. Q is hanging freely below the table and the system is on the point of slipping. Determine the coefficient of friction and find the extension of the string.
A particle of mass 2kg is being held in equilibrium on a smooth slope by a horizontal force, P, and a light, elastic spring. The spring has modulus of elasticity 10N as is attached to the particle and also to the slope 1.5m up the slope from the particle. If the slope is inclined at 25º, and the force P is of magnitude 5N, find the two possible natural lengths of the spring.
A particle of mass km is placed on top of a light, vertical spring of natural length 2a. The modulus of elasticity of the spring is 3mg and the spring is standing upright so that it lies in a vertical plane.
- Find the compression in the spring in terms of k and a;
- Find the value of k such that the length of the spring is halved due to the weight of the particle.

Answers

(a.) 0.45m, (b) 75N, (c) 1N
0.125m or 12.5cm
15mg N
5mg N
1.93m
𝞴 = 76.9N
(a.) Proof, (b) 7√3 gN
µ = 3/4, x = 1.2m
1.22m and 1.08m
(a) 2ka/3 (b) k = 3/2

Hooke’s Law Exercise 1 Worked Solutions

Elastic Potential Energy

Stretching or compressing an elastic string or spring stores elastic potential energy (“EPE”) in the system.

If an elastic string is stretched, the work required to stretch the string is related to the force applied and the length of the extension, x.

As work done equals force multiplied by distance, we can write $W = \int^{x_2}_{x_1} F dx$ .

Here the force is being applied over distance $x_2 - x_1$ . If we use $\frac{ \lambda x}{l}$ as the force, then the work done in stretching the string is $\int^x_0 \frac{ \lambda x}{l} dx$ = $[\frac{\lambda x^2}{2l}]^x_0$ .

So, the work required can be written as EPE = $\frac{\lambda x^2}{2l}$ , with the unit Joules.

Worked Example 1

Find the elastic energy in each of the following systems:

(a.) A light elastic string of natural length 2m and modulus of elasticity 100N is stretched by 1.2m;

(b.) A light elastic string of natural length 1.8m and modulus of elasticity 50N is compressed by one third of its original length;

(c.) A light spring of natural length 3a and modulus of elasticity 4mg is stretched to 5a.

Some questions may be more complicated. Let’s consider a particle of mass 4kg tied to two light elastic strings, a top string with natural length 1m and modulus of elasticity 3g N and a bottom string with natural length 1.2m and modulus of elasticity 2g N.

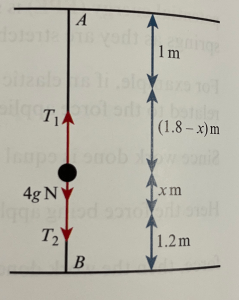
To determine the elastic energy stored in the system, we need to find the extension of each string. As AB is 4m, we can work out the middle part and then determine x.

NII⬆ gives $T_1 = T_2 + 4g$ .

Using Hooke’s law on each string and equating the forces gives $\frac{3g(1.8-x)}{1} = \frac{2gx}{1.2} + 4g$ . This leads to x = 0.3m

Adding the EPE stored in each string gives: EPE = $\frac{3g \times 1.5^2}{2 \times 1} + \frac{2g \times 0.3^2}{2 \times 1.2} = 34.5J$

Worked Example 2

Two points, A and B, lie on a smooth horizontal surface a distance 5a apart. A light, elastic string, of natural length 2a and modulus of elasticity 3mg, is attached to A and then attached to a particle, P, of mass m. A second light, elastic string, of natural length 1.5a and modulus of elasticity 7mg is attached to B and then attached to the same particle P. Determine the amount of EPE stored in the system.

Worked Example 3

A light, elastic string of length 2.5m has modulus of elasticity 65N. Find the work done when stretching the string from 3m to 6m.

Worked Example 4

A light, elastic string, of natural length 2a and modulus of elasticity 7mg, has one end tied to a point on a ceiling. The other end of the string is attached to a particle, P, of mass m. A second light, elastic string, of natural length 3a and modulus of elasticity 5mg, is tied to P. Its other end is attached to a second particle, Q, of mass 3m. Q is vertically below P.

With the system resting in equilibrium, both strings are taut. Find the elastic potential energy stored in the system.

Exercise 2

A light elastic string of natural length l and modulus of elasticity 𝞴 is stretched by an extension x, by means of a force T, causing the string to gain elastic potential energy (“EPE”). Find the unknown value in each case:
- 𝞴 = 50N, x = 0.5m, l = 1.5m. Find the energy stored in the string;
- EPE = 100J, 𝞴 = 60N, l = 1.2m. Find the extension of the string;
- EPE = 50J, x = 0.8m, l = 1.6m. Find the modulus of elasticity.
Prove, using integration, that the elastic potential energy stored in a string of natural length l and modulus of elasticity 𝞴 is $\frac{\lambda x^2}{2l}$ , where x is the extension of the string.
A particle of mass 5kg is attached to one end of a light elastic string of natural length 0.8m. The other end of the string is attached to a fixed ceiling and the particle is allowed to rest, hanging in equilibrium. If the string is stretched by an additional 80%, determine the modulus of elasticity. Hence find the elastic potential energy stored in the string.
A particle of mass 3kg is attached to one end of a light, elastic string of natural length 1.2m. The other end of the string is attached to a fixed ceiling and the particle is allowed to rest, hanging in equilibrium. If the string is stretched by an additional 50%, determine the modulus of elasticity and, hence, find the elastic potential energy stored in the string.
The points A and B are 4.5m apart, with A vertically above B. Particle P, of mass 2kg, is connected to A and B by means of two light, elastic springs. The spring attached to point A has natural length 1m and modulus of elasticity 50N; the spring attached to B has natural length 1.4m and modulus of elasticity 80N. The system rests in equilibrium. Find the EPE stored in the system.
A light elastic string has one end attached to a ceiling. The other end is attached to a particle of mass 3m. The string has natural length 2a and modulus of elasticity 6mg. The particle rests in equilibrium.
- Show that the extension in the string is a;
- A smaller particle of mass km is attached to the existing particle. If the EPE increase is $\frac{8}{3} mga J$ , find the value of k.
A light elastic string of natural length 2.4m is stretched between two points, A and B, on a horizontal ceiling. The distance AB is 4m. The modulus of elasticity of the string is 60N. A particle of mass 3.5kg is attached to the midpoint of the string. The system rests in equilibrium, with both parts of the string making an angle of 30º with the ceiling.
- Find the extension of the string;
- Determine the amount of elastic potential energy stored in the string.
A light, elastic string, of natural length and modulus of elasticity 2mg, is attached to a ceiling at the point A. The other end is attached to a particle, P, of mass 5m. A second light, elastic string, of natural length and modulsu of elasticity 8mg, is attached to P. The other end of this string has a particle, Q, attached to it. The system is allowed to rest in equilibrium. Given that the mass of Q is 3m, find
- The distance AQ;
- The amount of elastic potential energy stored in the system.

Answers

(a.) 4.17J. (b) 2m (c) 250N
Proof
𝞴 = 62.5N, EPE = 16J
𝞴 = 6g , (9/10)g J
134.6J
(a) Proof. (b) k=2
(a) 1.4m. (b) 24.5J
(a) (175/16)a (b) (813/32)mga J

Hooke’s Law Exercise 2 Worked Solutions

Work Energy principle

If a constant force acts on a body over a given distance, then the work done by the force is equal to the energy gain of the object.

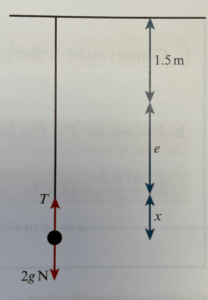
Now we consider systems that don’t rest in equilibrium, but are extended beyond their equilibrium, causing a rebound movement.

Consider a particle of mass 2kg attached to a light, elastic string of natural length 1.5m and modulus of elasticity 4g N.

The string is attached to a ceiling at its other end. The particle starts in equilibrium and then is pulled down a further 0.5m and released.

Suppose we wish to know the speed of the particle after it has travelled 0.4m upwards. We consider KE, GPE and EPE at the start and end.

First we must find the initial extension of the string, e. Using Hooke’s Law we get $2g = \frac{4g \times e}{1.5}$ , and so e = 0.75m.

Let the initial point have PE = 0. It also has KE = 0 and $EPE = \frac{4g \times (0.75+0.5)^2}{2 \times 1.5} = \frac{25}{12} g J$

At the final point, PE = 2g x 0.4, KE = ½ x 2v², and $EPE = \frac{4g \times (1.25-0.4)^2}{2 \times 1.5} = \frac{289}{300} g J$

By conservation of energy, $\frac{25}{12} g = v^2 + 0.8g + \frac{289}{300} g$ and so $v^2 = \frac{8}{25} g$ , giving $v = \frac{ 2 \sqrt{2g}}{5} ms^{-1}$ , which is about 1.79ms^-1.

Worked Example 1

A light elastic string, with natural length 2m and modulus of elasticity 60N, has one end attached to a point, A, on a rough horizontal surface. The other end is attached to a particle, P, of mass 3kg on a table. The particle is pulled to the side so that the distance AB is 4m.

a.) If the coefficient of friction between the table and the particle is 0.4, find the speed as the particle passes the point A;

b.) Find the initial acceleration.

Worked Example 2

A smooth disc with radius 1.2m is fixed to a horizontal plane. The centre of the disc is O. A light elastic string with natural length 0.8m and modulus of elasticity 100N is attached to the centre O, and the other end of the string is attached to a particle of mass 0.5kg. The particle is describing horizontal circles with constant angular speed.

Given that the particle is on the point of falling off the edge of the disc, find the angular speed of the particle and the total energy in the system.

Worked Example 3

A rough slope is inclined at an angle of 15º to the horizontal. A light elastic string is attached to the top of the slope at the point A. The string has natural length 2.4m and modulus of elasticity 150N. A particle of mass 1kg is attached to the other end of the string.

The particle is allowed to rest in equilibrium on the slope with the string taut.

a.) Find the extension of the string;

b.) The particle is pulled down a further 0.5m and released. Given that the coefficient of friction between the particle and slope is 0.4, find the distance of the particle from A when the particle first comes to instantaneous rest.

Worked Example 4

A particle of mass 2kg is attached to one end of a light elastic string of natural length 1.5m and modulus of elasticity 50√3 N. The other end of the string is attached to a point, O, on the ceiling. The particle describes horizontal circles with the string taut and 30º to the vertical. Find the angular speed of the particle.

Worked Example 5

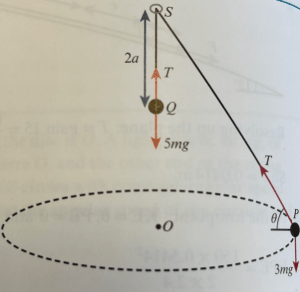
A particle, P, of mass 3m, is attached to one end of a light elastic string of natural length 5a and modulus of elasticity 8mg. The other end of the string is threaded through a small smooth ring S and a second particle Q of mass 5m is attached to this end. The particle P describes horizontal circles with angular speed ω. Particle Q remains stationary at a distance of 2a below the ring.

Find the extension of the string and the angular speed of Q.

Exercise 3