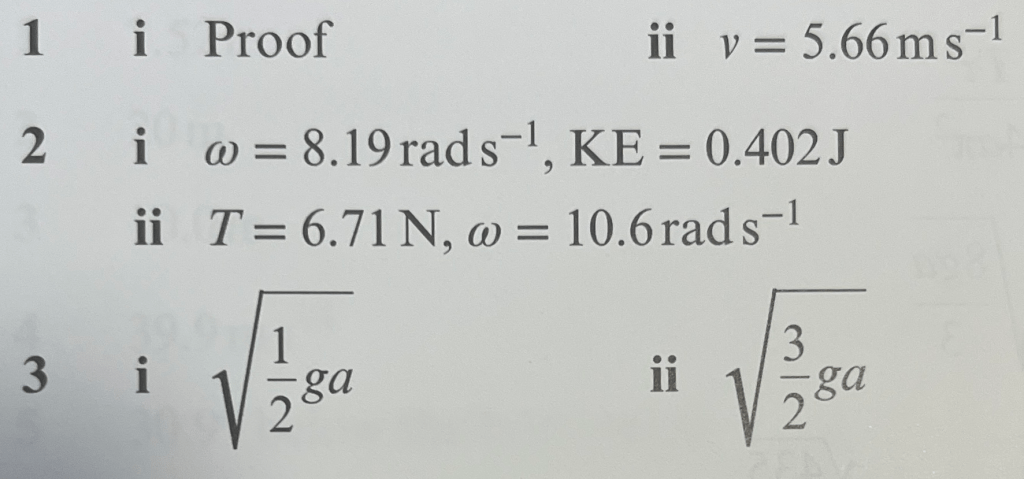We will now consider motion in horizontal and vertical circles.
We will come to understand that a particle moving in a circle is effectively continuously accelerating towards the centre.
Horizontal Circular Motion
If a particle moves at constant speed in a horizontal circle, the path it follows is along the arc of the circle, measured as r𝜽. Over time, the rate of change of the distance travelled is which is the same as
.
So . We call
the angular speed, denoted by ω. And so the linear speed of a particle moving in a circle is v = rω.
The angular speed, ω, is measured in radians per second (rads-1). As a complete circuit is 2π radians, so the number of revolutions per second (also called the frequency) is .
Worked Example. Angular and Linear Speed
In each case below, either convert angular speed to linear speed or linear speed to angular speed, or calculate both quantities, as appropriate:
- A particle travelling in a circular path of radius 5m with angular speed 4 rads-1;
- A particle travelling along a circular path of radius 2.5m with speed 4ms-1;
- A particle travelling on a circular path with radius 2m, where the time to cover one complete circle is 6s;
- The Earth travelling around the Sun, where the path is assumed to be circular and of radius 1.496 x 1011m.
The direction of motion of an object travelling in a circle is constantly changing.
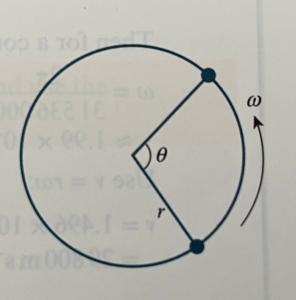
Let us consider two points on the path of a circle, P and Q;
We will let the angle POQ be very small and call it 𝛿𝜽. At point P the particle is moving at linear speed v. As Q is very close to P, we can assume that the speed at Q has components parallel and perpendicular to the tangent at P of vcos𝛿𝜽 and vsin𝛿𝜽.
Using the fact that sin𝛿𝜽 ≃ 𝛿𝜽 and cos𝛿𝜽 ≃ 1 we will consider the acceleration parallel and perpendicular to the tangent at P.
As acceleration is change in velocity over change in time, so the parallel component of acceleration is which is about
which is equal to zero.
However the perpendicular component of acceleration, acting towards the centre is , which is about equal to
. So the acceleration acts towards the centre with magnitude
, commonly written as
or
Worked Example
In each case, find the force towards the centre:
- A particle of mass 1.5kg, travelling with angular speed 4 rads-1, where the radius is 0.5m;
- A particle of mass 4kg, travelling with speed 5ms-1, where the radius is 2.4m;
- A particle of mass 0.5kg, travelling around a circle of radius 20m in 12s.
Worked Example 2
A particle is describing circles on a smooth horizontal table. The particle is attached to a light inelastic string that is attached to a point O where the radius of the circles is 1.2m. If the tension in the string is 40N and the particle can complete one circle in s, find the mass of the particle.
Worked Example 3
A particle is placed on a rough horizontal disc 4m from the centre of the disc. The particle has mass 2kg and the coefficient of friction between the particle and the disc is 0.6. The disc begins to spin around slowly until the particle slips. Find the frictional force on the particle when the disc is spinning at 2ms-1. Find also the angular speed of the disc when the particle is on the point of slipping.
Worked Example 4
Two particles are attached to a light, inelastic string of length 4a. One particle, P, or mass m, is placed on a large, smooth disc. The string is then threaded through a smooth hole in the centre of the disc. At the other end of the string is the particle Q, of mass 2m. The disc is spinning such that particle Q does not move and is 1.5a below the centre of the disc. Find the tension in the string and find the angular speed of the particle P in terms of a as it moves in circles.
Worked Example 5
A particle P, of mass 3kg, is placed on a large rough horizontal disc. P is then attached to a light inextensible string of length 2.4m. The string passes through a smooth hole in the centre of the disc and at the other end is a particle Q of mass 6kg. The coefficient of friction between P and the disc is 0.5. Q is hanging freely under the hole in the disc. The disc begins to spin with P at a distance of 1.6m from the centre of the disc. If Q does not move at any point during the motion, find the range of angular speeds possible.
Exercise 1
- In each of the following, use the relation
to determine the unknown value:
- v = 4, r = 6, find
;
- v = 6,
= 3, find r;
- r = 5
= 0.8, find v.
- v = 4, r = 6, find
- A particle of mass 0.2kg is attached to a light inextensible string of length 1.5m. The particle is moving in horizontal circles. Find the tension in the string if the speed of the particle is 5ms-1.
- A particle of mass 0.8kg is attached to a light inextensible string of length 1.2m. The particle is moving in horizontal circles. Find the angular speed of the particle if the tension in the string is 10N.
- A particle is describing horizontal circles on a smooth, horizontal table. The particle is fixed to its circular path by an inelastic string of length 1.5m. Given that the tension in the string is 45N, and that the mass of the particle is 5kg,
- Find the angular speed of the particle.
- State how many seconds the particle takes to describe one complete circle.
- A particle is placed on a rough horizontal disc, 2a from the centre of the disc. The particle has mass 3m. The disc then starts to spin at an angular speed of
. Given that the particle is on the point of slipping, find a range of values of
such that equilibrium is not broken.
- A car is driving on a horizontal circular section of road that has radius 50m. The car is of mass 800kg and the coefficient of friction between the tyres and the road is 0.8. Find the maximum speed that the car can drive around the road without slipping.
- A particle of mass 1.5kg is resting on a smooth horizontal table. The particle is attached to a light, inextensible string of length 2.5m. The string is passed through a smooth hole in the table. At the other end of the string is a particle of mass 4kg. The particle on the table is set in motion and describes circles with radius 1.5m. Find the speed of the particle on the table. Assume that the particle that is freely hanging does not move during the motion.
- A particle with mass m is describing horizontal circles of radius a. Given that the particle can complete one circle in
seconds, and that the particle is held in its path by means of a light, inextensible string with tension T, find an expression for the mass m.
- A particle is placed on the inside of a rough, hollow cylinder of radius 2a. The cylinder is placed upright and can rotate about an axis through its centre. The particle has mass m and the coefficient of friction between the particle and the inside of the cylinder is
. Given that the particle does not slip as the cylinder rotates find the speed (in metres per second) at which the cylinder rotates.
- A particle, P, is placed on a large, rough, horizontal disc. P is of mass 2.4kg. The particle is then attached to a light inextensible string of length 4m. The string passes through a smooth hole in the centre of the disc, and at the other end is a particle Q of mass 3kg. The coefficient of friction between P and the disc is 0.2. Q is hanging freely under the hold in the disc. The disc is set spinning with P at a distance of 1.2m from the centre of the disc. If Q does not move at any point during the motion, find the range of speeds possible.
Answers to Exercise 1
- (a) 2/3 rads-1 (b) 2m (c) 4ms-1
- 10/3 N
- 3.23 rads-1
rads-1, 2.57s
- 20ms-1
ms-1
Worked Solutions to Exercise 1
3 Dimensions
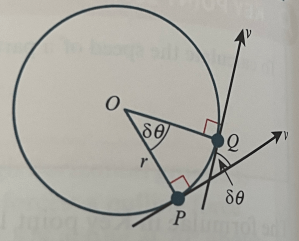
We consider now the conical pendulum model, with a light inelastic string with one end attached to a fixed point O and the other end having a particle following small horizontal circles, as in the diagram below:
The force acting towards the centre of the horizontal circle is now a component of the tension in the string. The weight is of course a vertical component to the tension in the string.
So using NII upwards, we have , giving us
Using NII horizontally we have
As , we can write this as
or simply
Combining the two equations above gives us
So, for instance, if a particle with mass 2kg is rotated at an angle of 30º by a string of length 2.5m, the tension in the string will be N and the angular speed will be
rad s-1.
Worked Example
A particle of mass 1.5kg is attached to one end of a light inelastic string of length 1.8m. The string is attached to a fixed point O at its other end. The particle is set in motion and describes horizontal circles with the string taut and at 20º to the downward vertical through the point O. Find the tension in the string and the angular speed of the particle.
Note that if a question requires the speed of the particle rather than angular speed then the NII horizontally gives and so the
terms don’t cancel.
Worked Example 2
A particle of mass 3m is attached to a light inextensible string of length 5a. The other end of the string is attached to a fixed point O. The particle is moving in horizontal circles about a centre that is 4a vertically below the point O. By resolving vertically and horizontally, find the tension in the string and the linear speed of the particle.
Consider now an object on a sloped surface (sometimes called a banked surface) as in the diagram below. Here, instead of tension in a string, the normal reaction force is relevant:

If the surface is smooth, the situation is analogous to the conical pendulum.
If there is friction, it typically acts down the slope, as excessive speed puts the car at risk of slipping up the slope. So we have:
NII vertically: ; and
NII horizontally:
If the car is on the point of slipping then and so the vertical NII gives
giving
Also the horizontal NII becomes , so
Dividing the fraction on the LHS through by gives
(this doesn’t need to be memorised, but you should understand its derivation).
Worked Example 3
A car of mass 1000kg is turning on a banked road of radius 80m. The incline of the road is 15º and the car is travelling at 25ms-1. The car is about to slip up the road.
a.) Resolve vertically and find an expression for the reaction force between the car and the road, in terms of the frictional force;
b.) Resolve towards the centre of the circle
c.) Find the coefficient of friction between the car and the road.
We may also face questions with more than one force acting towards the centre, as in the example below. We tackle this example by assuming that a single string attached to the centre can be represented as two separate strings with different tensions.
Worked Example 4
A light inelastic string of length 2a is tied to a fixed vertical pole at two points, A and B. A is a distance a vertically above B. A particle of mass 2m is attached to the midpoint of the string. The particle is then set in motion to describe horizontal circles. Both parts of the string are taut at all times during the motion.
Given that the speed of the particle is find the tension in both parts of the string.
Exercise 2
1.) A particle of mass 0.9kg is attached to a light inextensible string of length 2.4m. The other end of the string is attached to a fixed point on the ceiling. The particle is describing horizontal circles with the string taut and making an angle of 25º with the downward vertical. Find the speed of the particle.
2.) A particle of mass 1.6kg is attached to a light inextensible string of length 1.4m. The other end of the string is attached to a fixed point on the ceiling. The particle is describing horizontal circles with the string taut and making an angle of 35º with the downward vertical. Find the angular speed of the particle.
3.) A particle of mass 2kg is attached to a light, inextensible string of length 3m. The other end of the string is attached to a fixed point on the ceiling. The particle is describing horizontal circles with the string taut and making an angle of 30º with the downward vertical. Find the angular speed of the particle.
4.) A car is driving around a banked road inclined at 15º to the horizontal. The car has mass 1200kg and the radius of the circular part of the road is 60m. The coefficient of friction between the road and the tyres is 0.75 and the car is on the point of slipping up the road. Find the speed of the car.
5.) A particle, P, of mass 3kg, is attached to two light, inextensible strings. One string is attached at its other end to a point, A. The other string has its other end attached to a point, B. A is 4m above B. The particle makes horizontal circles such that angle PAB is 30º and angle PBA is 60º. Given that the speed of the particle is 3.6ms-1, find the tension in each string.
6.) A hemispherical bowl of radius a is resting in a fixed position where its rim is horizontal. A small ball of mass 2m is moving around the inside of the bowl such that the circle described by the ball is a/2 vertically below the rim of the bowl. Find the speed of the ball.
7.) A light, inextensible string of length 4m is threaded through a smooth ring at the point O. One end of the string has a particle, P, of mass 4kg, which is 1.2m vertically below O. Particle Q, of mass 1.6kg, is attached to the other end of the string. Particle Q is describing horizontal circles, with the string OQ making an angle of 20º with the downward vertical.
a.) If particle P does not move during the motion, find the angular speed of Q.
b.) Find the number of complete circles described per minute.
8.) A car is moving on a circular section of road where the road is banked at 25º to the horizontal. The radius of this section of road is 100m. The car has mass 1400kg and is travelling at 30ms-1. Given that the car is about to slip up the road, find the value of µ.
9.) A toy plane of mass 0.4kg is attached to one end of a light, inextensible string of length 6m. The other end of the string is attached to the point O. The string is taut and makes an angle of 45º with the upward vertical. Find:
a.) The tension in the string;
b.) The speed of the toy plane.
Answers
1.) 2.17 ms-1
2.) 2.95 rads-1
3.) 1.96 rads-1
4.) 27.65 ms-1
5.) TAP = 37.2N, TBP = 4.44N
6.)
7.) (a.) = 2.99 rads-1 (b) 28.5 per minute
8.)
9.) (a.) (b.) 6.51ms-1
Circular Motion Exercise 2 Worked Solutions
Vertical Circular Motion
Now we start to consider particles describing vertical circles as in the diagram below:
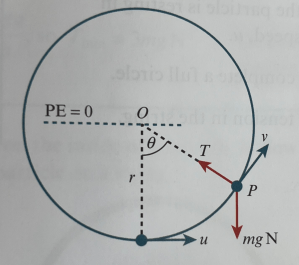
Here there will be a change in potential energy due to the height, which leads to an inverse change in kinetic energy.
We consider a particle with mass m attached to a light inelastic string of length r. It is initially at rest in equilibrium, then projected with speed u from its lowest point. We assume no resisting forces and so use the principle of conservation of energy.
As shown in the diagram, we set potential energy as zero in the centre of the circle.
So PE0 = -mgr and KE0 =
At any other position on the circle, PE1 = -mgrcos𝜽 an KE1 =
In order to complete a full circle, KE at the top of the circle must be greater than zero.
If we use NII towards the centre from a general point, T – mgcos𝜽 =
Using conservation of energy we have
Combining the two equations gives . From this we can also see that if T≥0 then
Also note that at the top of the circle 𝜽 = 180º and so . This gives us the key condition for a particle to complete vertical circles, which is that u ≥ √(5gr).
Worked Example
A particle of mass m is attached to a light inelastic string of length 2a. The other end of the string is attached to a fixed point O. When the particle is resting in equilibrium below the point O, it is given a horizontal speed u.
a.) Write down the minimum value of u required to complete a full circle;
b.) Given that u2 = 16ga, find the greatest and least tension in the string.
A small ball placed on the inside of a hollow ring is analogous to the particle on string, with a reaction force instead of the tension in the string, as shown in the diagram below. If a particle lack sufficient energy to reach the top, but passes the centre of the circle, it will leave the surface of the ring and become a projectile. If it lacks sufficient energy to pass the centre, it will behave instead like a pendulum.
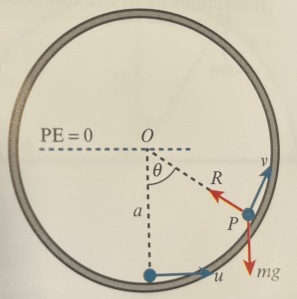
Worked Example 2
A particle P of mass m is resting on the inside of a smooth circular ring with centre O and radius a. The particle is projected from the lowest point with a horizontal speed of . Find the angle between the line OP and the downward vertical at the point where the particles leaves the surface of the ring.
Worked Example 3
A particle P of mass m is resting on the inside of a smooth circular ring with centre O and radius a. The particle is projected from the lowest point with a horizontal speed of u2 = 3ga. Find the greatest height above O achieved by the particle.
A particle could also travel on the outside of a vertical circle as shown in the diagram below. Here the particle is given a slight push to start it moving and we consider when it will leave the surface of the hemisphere drawn:
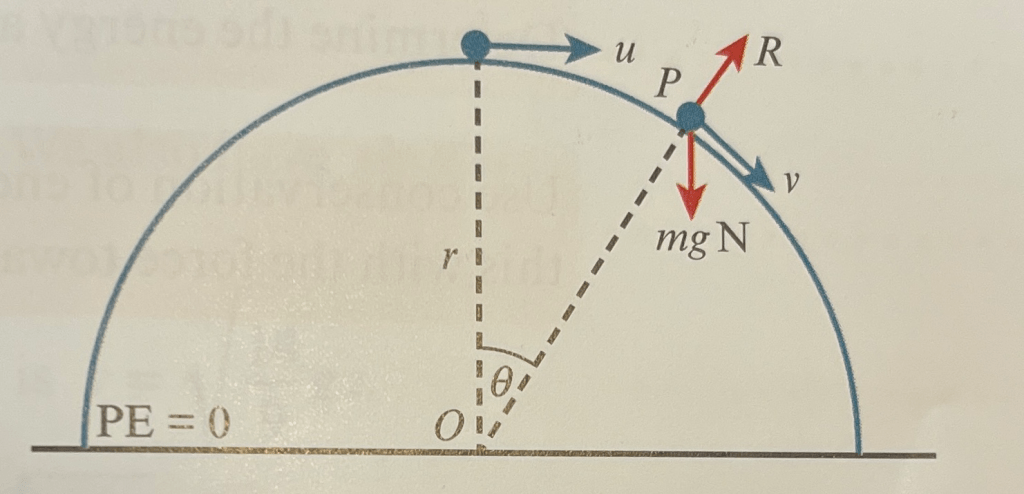
Here and
and at a general point,
and
.
Rearranging conservation of energy gives
Multiplying through by 2/r gives:
Using NII towards the centre of the hemisphere gives , which combines to give
When the particle leaves the surface, R=0, so . This is a useful result, as it tells us that if u is almost zero, then cos𝜽 is almost 2/3, so with a slight push the particle will leave the surface after 48.2º.
It also shows us that if u2 = gr then cos𝜽 = 1 and so 𝜽=0, which implies that the particle leaves the surface immediately if given an initial speed of √(gr)
Worked Example 4
A particle of mass m is projected from the top of a hemisphere of radius a.
The hemisphere has its plane face in contact with the horizontal surface below it and is to be considered smooth.
If the initial speed at the top is , find the speed of the particle at the moment it loses contact with the hemisphere.
Worked Example 5
A smooth hemisphere of radius 2a is fixed with its plane face against a horizontal surface. The centre of the plane face is denoted as O. A particle of mass m is placed at the top of the hemisphere. The particle is then projected horizontally with speed . The particle first lands on the horizontal surface at the point B. Determine the distance OB.
Excercise 3
1.) A particle of mass m is attached to the end of a light inelastic string of length 1.5a. The other end of the string is attached to a fixed point O. When the particle is resting in equilibrium it is given a horizontal speed of . Find the angle turned through when the particle comes to instantaneous rest.
2.) A particle of mass m is attached to the end of a light inelastic string of length 1.2a. The other end of the string is attached to a fixed point O. When the particle is resting in equilibrium, it is given a horizontal speed of . Find the angle turned through when the tension in the string is zero.
3.) A smooth hemisphere of radius 1.6a is placed plane face down and fixed onto a horizontal plane. A particle of mass 2m is placed on the top of the hemisphere and projected with speed . As the particle travels down the curved surface of the hemisphere it turns through an angle 𝜽, where 𝜽 is measured from the vertical through the centre of the hemisphere. Find the value of 𝜽 when the particle loses contact with the hemisphere.
4.) A particle of mass 2m is attached to the end of a light inelastic string of length a. The other end of the string is attached to a fixed point O. When the particle is resting in equilibrium, it is given a horizontal speed of and consequently describes vertical circles. Find the greatest and least tension in the string.
5.) A particle of mass m is attached to a light inextensible string of length a. With the other end of the string attached to a fixed point, A, the particle rests in equilibrium. The particle is then given an initial horizontal speed u. Find the condition on u such that the particle never leaves the circular path, but never completes full circles.
6.) A particle of mass 3kg is resting on the inside of a smooth circular hoop of radius 2m. From the bottom position the particle is projected horizontally with speed 8ms-1. Find the greatest height achieved by the particle from the point where it is projected.
7.) A smooth hemisphere of radius 1.5a is placed plane face down and fixed onto a horizontal plane. A particle of mass m is placed on the top of the hemisphere and projected with speed . As the particle travels down the curved surface of the hemisphere the particle turns through an angle 𝜽. Find the value of 𝜽 when the particle loses contact with the hemisphere.
8.) A particle of mass m is resting on the inside of a smooth circular hoop of radius 3a. The particle is then projected form the lowest point with horizontal speed u.
8a.) State the minimum speed required to complete vertical circles.
8b.) The particle is projected with speed . Find the speed when the particle has turned through 120º.
8c.) Find also the reaction force exerted on the particle when the angle is 120º.
9.) A particle is held at rest on a smooth circular track which is an arc of radius a. The track is standing in a vertical plane and is fixed to a horizontal surface. The points O and A are such that OA is horizontal, as shown in the diagram below:
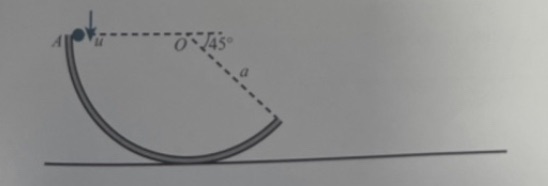
The particle is release from rest and proceeds to slide down the track.
9a.) Find the speed of the particle at the point where it is just about to lose contact with the track.
9b.) Find the greatest reaction force on the particle while it is in contact with the track.
10.) A string of length 2a is attached to a point O and has a particle of mass 3m attached to the other end. The particle is resting in equilibrium. The particle is then projected with horizontal speed 1
10a.) Find the speed of the particle at the highest point of its circular path.
10b.) Find the difference between the greatest and least tension in the string.
Answers

Circular Motion Exercise 3 Worked Solutions
Mixed Exercise

Answers