We can call the trigonometric functions circular functions, because they are derived from the unit circle.

Remember the four different kinds of conic section:

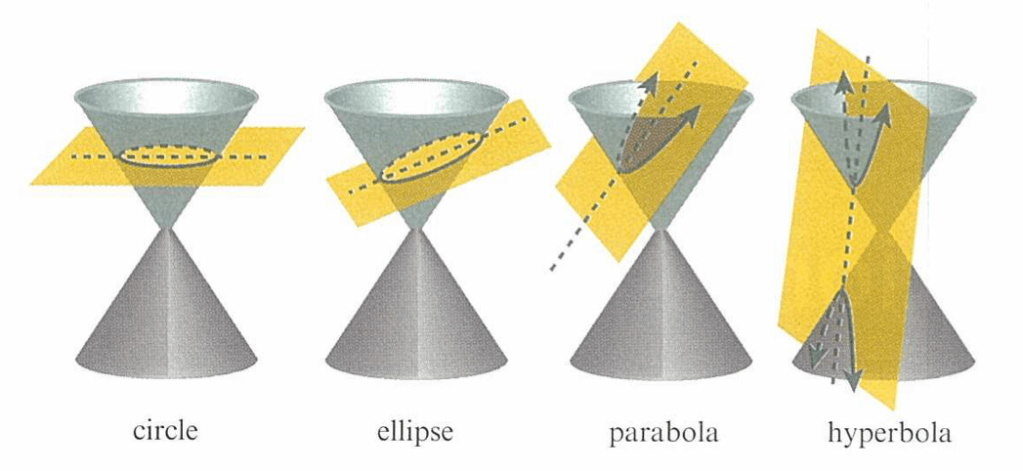
We will look now at hyperbolic functions, derived from the unit hyperbola. They can be useful for finding efficient solutions to differential equations.

We will start by definition the hyperbolic functions in terms of the exponentials.

“Shine Ex”

We can think of the graph as the average of y = e^x and y = -e^-x

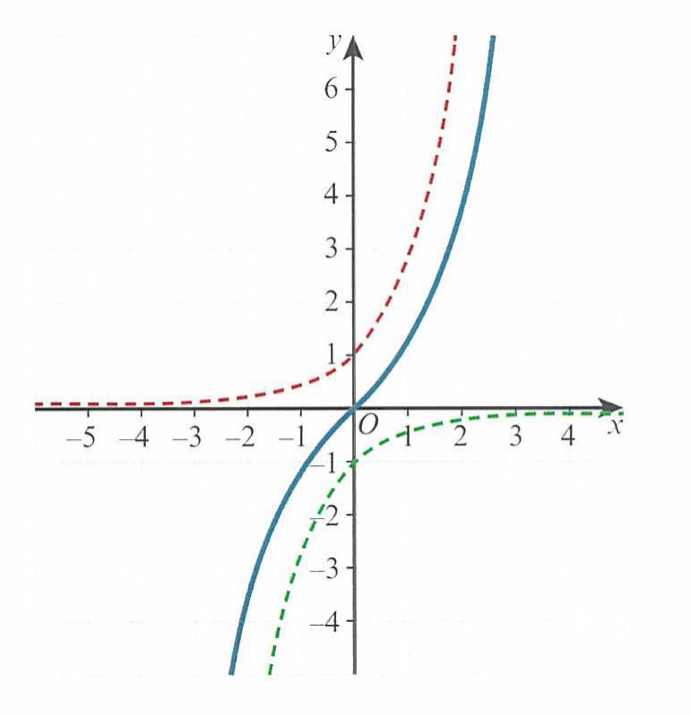
Looking at the graph, we notice that the function is a one-to-one mapping whose domain and range is the set of real numbers. We also notice that it is an odd function.

“Coshine Ex”

We can think of the graph as the average of y = e^x and y = e^-x

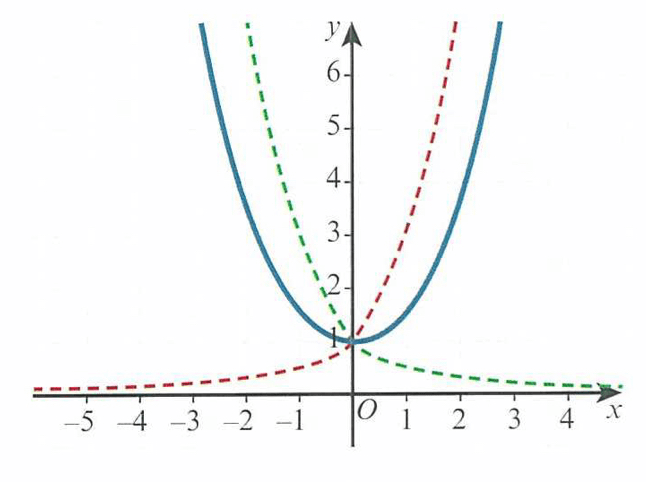
Here we see that the function is not a one-to-one mapping. Also its domain is the set of all real numbers, its range is f(x) ≥ 1 and it is an even function. In order to make it into a one-to-one function (i.e. so it has an inverse), we restrict the domain to x ≥ 0.

Looking at the definitions of sinh x and cosh x we notice that sinh x + cosh x = e^x.

Below are the four remaining hyperbolic functions:

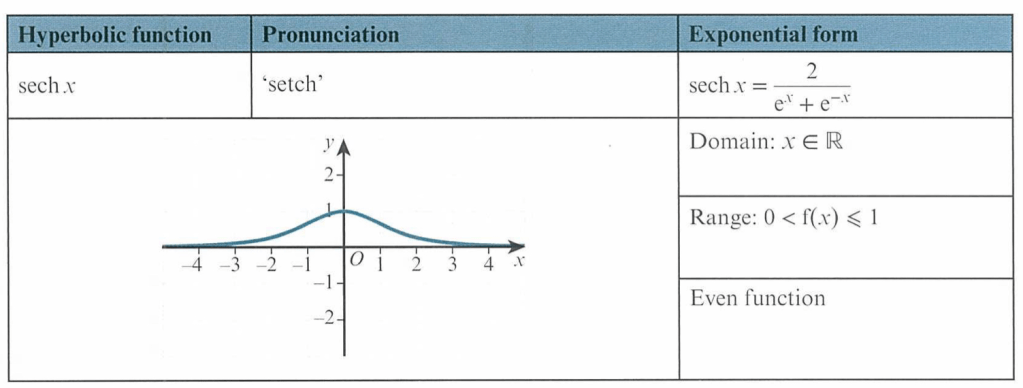
Worked Examples

• Sketch the graph of y=|3cosh(x+1) – 4| ;
• Solve 4coshx – 3sinhx = 4, leaving your answer in exact form;
• Solve 3tanh²x – 4tanhx = 4.

Exercise

Answers

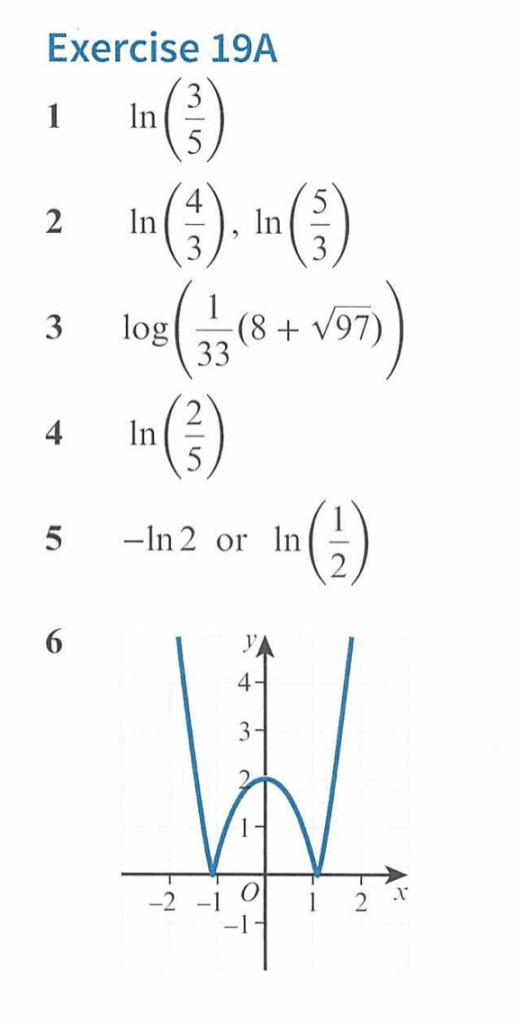
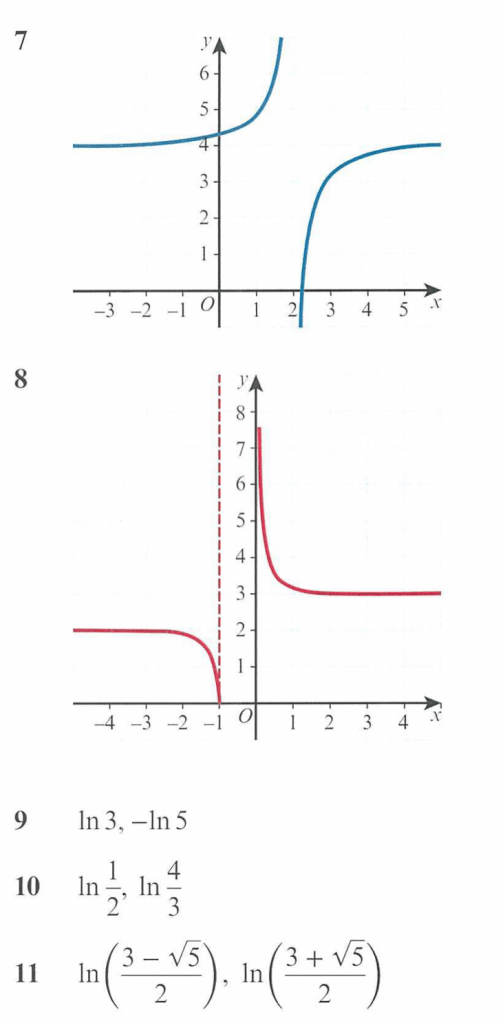
Worked Solutions (exercise 19A)

Hyperbolic Identities

If we write out sinhx and cosh x in terms of their exponential definitions, it is straightforward to prove that cosh²x – sinh²x = 1. But we should also memorise it.

We can use the same approach to prove that sinh(A+B) = sinhAcoshB + sinhBcoshA.

In general, to change a trigonometric identity to a hyperbolic identity, we switch the sin’s to sinh’s , the cos’s to cosh’s and change the sign whenever there is a product of sinhs. Note, that this doesn’t constitute a proof, but can help us if we are not asked for a proof.

Using Osborne’s rule, we can see that the trigonometric identity gives the hyperbolic identity .

Exercise

Worked solutions (exercise 19B)

Inverse Hyperbolic Functions

As with any function, the inverse functions of the hyperbolic functions are a reflection in the line y=x of the one-to-one part of the functions.

Worked example

Solve the equation sinh²x – 5sinhx + 4 = 0

Logarithmic form for inverse hyperbolic functions

Note that, using logarithms, we can write the inverse hyperbolic functions as exact values.

Worked example

Find the logarithmic form of sinh^-1x

For your ease, the logarithmic forms of the inverse hyperbolic functions are given below. Why not memorise them, then they will be part of your knowledge for life? You must also be able to derive them if a question asks you too.

Worked Examples

Solve the equation sinh²x – 5sinhx + 4 = 0

Exercise and General Exercises

Answers

Worked Solutions (Exercise 19C and EOC exercise 19)