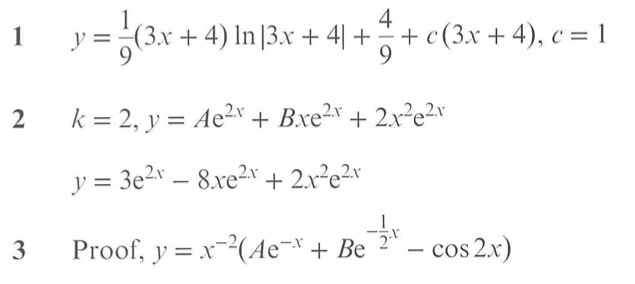9231. FP2. Differential Equations

What is a differential equation?

What does it mean to solve them? (What is the difference between the general solution and a particular solution)

We can already solve DEs of the for y’=f(y)g(x)

What if we get something like xy’+y=x?

We can’t expect to always find DEs looking like the product rule. What about y’+3y=e^-3x?

Any first order DE that is linear in y can be rewritten as y’+f(x)y=g(x).

We want the LHS to be in the form: u’v+uv’. To get it in this form we simply need to multiply through the whole equation by the integrating factor I(x)=e^∫f(x)dx

Why does it work?

y’+f(x)y=g(x)
=> I.y’ +f(x).I.y = I.g(x)
We want I such that I’=f(x).I,
=> $\frac{ \acute{I} }{I} = f(x)$
=> $\int \frac{\acute{I} }{I} dI = \int f(x) dx$
=> ln(I)= ∫f(x) dx
=> I=e^{∫f(x) dx}

This method was developed by Leonard Euler around 1730 (the separating variables method had previously been developed by his teacher, Johann Bernoulli).

Worked Example 1

Find the general solution of the differential equation: $cot(t) \frac{dy}{dt} + y = cosec t - sin t$

Worked Example 2

Find the particular solution of the differential equation: $t \frac{dx}{dt} + 3x = t^2 + 1$ with initial conditions x=1, t=1.

Worked Example 3

Solve the differential equation $\frac{dy}{dt} + ycoth(t) = 2e^{3t}$ for initial conditions y=0, t=0.

Exercise 1

Answers

Exercise 1 Worked Solutions

Second Order ODEs

Consider ay’’+by’+cy=0

It is a linear combination of multiples of a function, its first derivative and its second derivative.

For these terms to all cancel out, we need a function whose first derivative and second derivative has the same form as the function itself. Which functions are suitable?

Putting in suitable constants, we take the function: y=Ae^tx

So y’=Ate^tx and y’’=At²e^tx

So ay’’+by’+cy = aAt²e^tx+bAte^tx+cAe^tx = 0

Notice that Ae^txfactors out, so we have at²+bt+c=0. We call this the auxiliary equation for the ODE and its solutions give us the ODE’s solutions

How many solutions can there be to the auxiliary equation at²+bt+c=0?

Suppose there are two solutions, t₁ and t₂. Then both the solutions y=Ae^t1xand y=Be^t1x (for arbitrary constants A and B) are solutions to the ODE. We can say in general that the linear combination of these: y=Ae^t1x+ Be^t1xis the general solution to the ODE.
Suppose there is one repeated solution, t₀. Then y=(A+Bx)e^t0xis the general solution to the ODE.

Why is the solution in this form?

Consider y’’-4y’+4y=0, with AE: (t-2)²=0.

Clearly y=Ae^2x is one solution. We know there should be another solution (and another arbitrary constant, so we can write y=f(x)e^2x and try to find out the function f(x))

y = fe^2x
=> y’= f’e^2x+2fe^2x
=> y’’=f’’e^2x+2f’e^2x+2f’e^2x+4fe^2x= f’’e^2x+4f’e^2x+4fe^2x
If we substitute these into our ODE, y’’-4y’+4y=0, we get:
y’’-4y’+4y=0
(f’’e^2x+4f’e^2x+4fe^2x) – 4(f’e^2x+2fe^2x)+4fe^2x =0
=>f’’=0
=> f’=c
=> f=cx+b. Which is why we use this form
This method was derived by D’Alembert around 1750.

But what if the solution is complex?

Then y=Ae^(a+bi)x+Be^(a-bi)x

So y=e^ax(Ae^(bi)x+Be^(-bi)x)

y=e^ax(Ae^(bi)x+Be^(-bi)x)

We can simplify this using Euler’s Formula: e^bix=cosbx+ibsinx

So y=e^ax(A(cosbx+isinbx)+B(cosbx-isinbx))

Gathering the cosines and sines together, we have: y=e^ax((cosbx(A+B)+sinbx(A-B))

Which is simply y=e^ax(Pcosx+Qsinx)

N.B. The note below explains why we are comfortable replacing Ai-Bi with a real number:

So, in general, we use the ODE to form the auxiliary equation and solve the auxiliary equation to find the general solution from the above.

We can then use initial conditions or boundary conditions to find out the particular solution (i.e. without any arbitrary constants)

Worked Example 1

Find the general solution of the differential equation $\frac{dy}{dx} + 3y = 0$

Worked Example 2

Find the general solution for the differential equation $\frac{d^2x}{dt^2} +3 \frac{dx}{dt} - 10x =0$

Worked Example 3

Find the general solution of the differential equation $\frac{d^2r}{dt^2} - 4 \frac{dr}{dt} + 4r = 0$

Worked Example 4

Find the general solution for the differential equation $8 \frac{d^2y}{dx^2} + 12 \frac{dy}{dx} + 17y = 0$

Worked Example 5

The second order differential equation $2 \frac{d^2y}{dx^2} + 7 \frac{dy}{dx} + 3y = 0$ has initial conditions y=0 and $\frac{dy}{dx} = \frac{5}{2}$ when x=0. Find the particular solution.

Worked Example 6

Given that the boundary conditions for the differential equation $\frac {d^2y}{dx^2} +8 \frac{dy}{dx} + 16y = 0$ are x=0 when y=1 and x=1 when y=0, find the particular solution.

Exercise 2

Answers

Exercise 2 Worked Solutions

Homegeniety

Have you noticed that for all of our second order differential equations, the right hand side of the equation was equal to zero?

What should we do if this isn’t the case? i.e. if the equation is non-homogenous?

First we should note that adding the general solution to the related homogenous equation to our solution will not change the solution (because it gives zero when put in the equation).

So our general solution to a non-homogenous equation will be of the form GS=CF+PI, where the solution to the related homogenous equation is now called the complementary function.

We find the particular integral relevant to the RHS of the equation by using a trial function, which is essentially a guess at the solution in the correct form, with constants in to be determined.

How to find the Particular Integral

Note that we need both trigonometric functions in our trial function because of the way differentiation cycles through these functions.

Special cases

In some differential equations the function on the right-hand-side has the same form as one of the complementary functions. For example, the complementary function of the differential equation $\frac{d^2y}{dx^2} - 5 \frac{dy}{dx} + 6y = 4e^{3x}$ is $Ae^{2x} + Be^{3x}$ and e^3x occurs on the right hand side. In this situation it is no good using the trial function ae^3x, since upon substituting y=ae^3x, $\frac{dy}{dx} = 3ae^{3x}$ and $\frac {d^2y}{dx^2} = 9ae^{3x}$ into the differential equation, you obtain 9ae^3x-5(3ae^3x)+6(ae^3x)=4e^3x => 0=4e^3x and so clearly this trial function doesn’t work. Instead we use $axe^{3x}$ as a trial function.

This illustrates a general rule. If the function on the right-hand-side of the differential equation has exactly the same form as one of the terms of the complementary function, you multiply the usual trial function by the independent variable to give a new trial function. In order to recognise these special cases when they arise, it is worth getting into the habit of finding the complementary function before the particular integral.

Worked Example 1

For $\frac{d^2y}{dx^2} + 4 \frac{dy}{dx} + 4y = 2 + x^2$ determine both the complementary function and the particular integral. Hence write the general solution.

Worked Example 2

Given that $\frac{d^2y}{dx^2} + 3 \frac{dy}{dx} +2y = e^{\frac{x}{2}}$ + 2x + 5, determine the general solution.

Worked Example 3

Find the general solution for $\frac{d^2h}{dt^2} - 2 \frac{dh}{dt} + h = 3sint$

Worked Example 4

Determine the general solution for the differential equation $\frac{d^2y}{dx^2} + 5 \frac{dy}{dx} + 4y = 3e^{-x}$

Worked Example 5

The differential equation $\frac{d^2y}{dt^2} + 8 \frac {dy}{dt} +16y = 2e^{-4t} + t$ has initial conditions $y=1$ , $\frac{dy}{dt} = 2$ , when $t=0$ . Find the particular solution.

(N.B. In this example, because e^-4t and te^-4t are both present in the complementary function, we need to use t²e^-4t within the particularl integral)

Worked Example 6

Determine the general solution for $\frac{d^2y}{dx^2} + y = e^{-4x}$ and explain what happens to this solution as x tends to infinity.

Exercise

Solutions

Exercise 3 Worked Solutions

Substitution methods for ODEs. Form: f(y/x)

If an ODE is of the form y’=f(y/x) we can use the substitution y=ux, which replaces y/x with u and y’ with u’x+u, giving an equation in separable form.

Worked Example. Form y/x

Using a suitable substitution, solve the differential equation $\frac{dy}{dx} = \frac{x-y}{x+y}$ , giving your answer in an appropriate form.

Form: F(ax+by)

ODEs of the form $\frac{dy}{dx} = F(ax+by)$ can generally be solved by using the substitution u = ax+by

Worked example. Form F(ax+by)

Using the substitution u = 3y + 2x, find a general solution for the differential equation $\frac{dy}{dx} = e^{3y+2x}$

Worked Example. Particular solution

Find the particular solution for the differential equation $y \frac{dy}{dx} = x - y^2$ , using the substitution $u = x-y^2$ and the initial conditions x=0, $y = \frac{1}{2}$

Substitution methods for second order ODEs

We can often use a substitution u=yx (where y is a function of x, to simplify a second order ODE (exam questions may give a specific alternate substitution).

If u=yx, then u’ = y’x+y and u’’=y’’x+2y’. We can rearrange these to put y in terms of u before substitution into an equation.

Worked Example. Second Order ODEs

Using the substitution y=ux, show that the differential equation $x^2 \frac{d^2y}{dx^2} + (3x^2-2x) \frac{dy}{dx} + (2x^2-3x+2)y = x^3e^x$ can be simplified to the equation $\frac{d^2x}{dx^2} +3 \frac{du}{dx} + 2u = e^x$

Substitutions which introduce a new variable

Some ODEs are best solved by introducing a new variable, e.g. x=e^t

We then use the fact that $\frac{dy}{dx} = \frac{dy}{dt} \frac{dt}{dx}$ and that $\frac{d^2y}{dx^2} = \frac{d}{dx} (\frac{dy}{dx}) = \frac{d}{dt} (\frac{dy}{dx}) \frac{dt}{dx}$

Worked Example. Introducing a Variable 1

The initial conditions for the differential equation $2y \frac{d^2y}{dt^2} - ( \frac{dy}{dt})^2 + 8y \frac{dy}{dt} + 16y^2 = 12y^{ \frac{3}{2}}t^2$ are y=1 and $\frac{dy}{dt} = 4$ , when t=0. Given that y>0, and using the substitution $z = y^{\frac{1}{2}}$ , find the particular solution of the differential equation in the form y=f(t).

Worked Example. Introducing a Variable 2

Using the substitution $x = \frac{1}{t^2}$ , show that the equation $4x^3 \frac{d^2y}{dx^2} + (6x^2+10x^{ \frac{3}{2}}) \frac{dy}{dx} +4y = \frac{1}{x}$ reduces to the equation $\frac{d^2y}{dt^2} - 5 \frac{dy}{dt} +4y = t^2$

Exercise

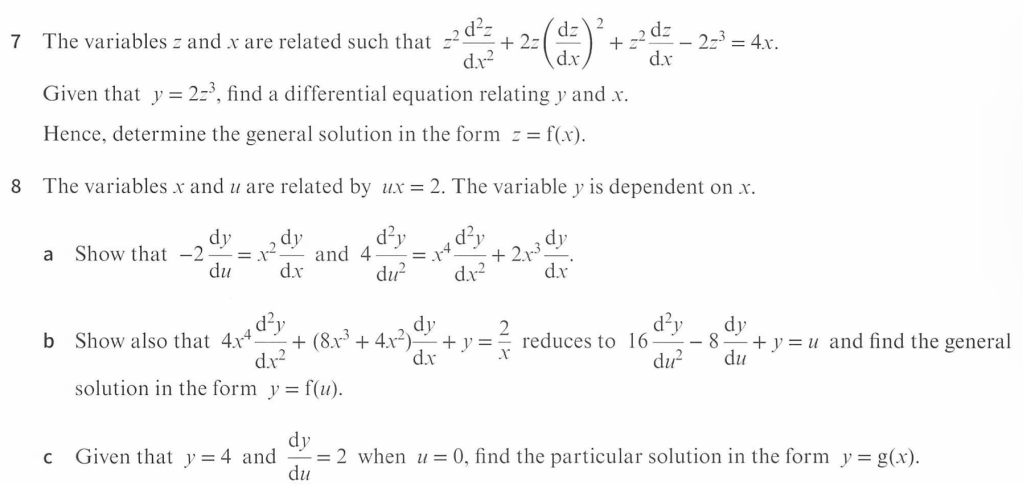
Notes for exams

With substitutions suggested in an exam, there is normally one way to have the substitution that is easier to differentiate (normally it is given in this form). After differentiating it the easy way, algebra can be used to rearrange it into the form needed to.

General Exercise

Answers

Exercise 4 & End of Chapter Exercise Worked Solutions

9231. FP2. Differential Equations

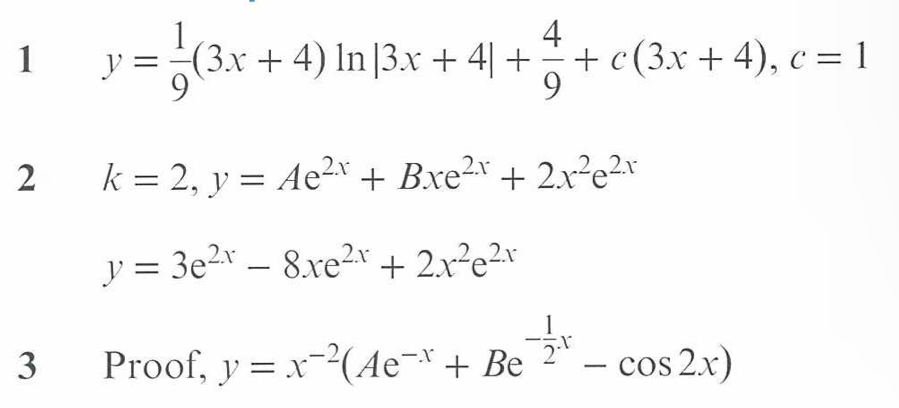
Share this: