From earlier work you should already know the following:
- Complex numbers in rectangular form: x+yi;
- Complex numbers in polar form (trigonometric & exponential);
- Arithmetic with complex numbers (remember that multiplication in polar involves multiplying the moduli and adding the arguments);
- Fundamental Theorem of Algebra: A degree n equation has n roots, all either real or in complex conjugate pairs.
Demoivre’s Theorem
If z=cos𝜽+isin𝜽, then zn=cos(n𝜽) + isin(n𝜽)
This can be proved using induction.
We can use DeMoivre’s theorem to calculate cos(n𝜽) or sin(n𝜽) as a sum of powers of cos𝜽 or sin𝜽, by using the Binomial Theorem to expand zn, using Pythagoras’ Theorem to change to just one trigonometric function, and then comparing real and imaginary parts.
This can also be used to solve certain equations in x by replacing x with a trigonometric function.
Worked Example 1 – Using DeMoivre’s Theorem
Find the value of:
(a)
(b)
(c)
(d)
Worked Example 2 – Expressing Trigonometric Functions of Multiple Angles
Express cos5𝜽 in terms of cos𝜽.
Express sin3𝜽 in terms of sin𝜽.
Express tan4𝜽 in terms of tan𝜽.
Worked Example 3 – Solving Polynomial Equations using Substitution
By considering the form of tan3𝜽, solve the cubic equation
Exercise 1
1.) Find the values of the following complex numbers: (a) , (b)
.
2.) Write cos4xcosx in terms of powers of cos x.
3.) Find the values of the following expressions, giving your answer as an exact value: (a) , (b)
, (c)
4.) Using de Moivre’s theorem, or otherwise, find in terms of
5.) Find in terms of
and hence solve the equation
6.) Show that can be written as
.
7.) Find in terms of
8.) Show that . Hence determine the solutions to the equation
9.) By considering that , find all solutions for the polynomial
Answers
1.) (a) , (b) -16 + 16i
2.) cos(x) – 8cos(x3) + 8 cos (x5)
3.) (a) , (b) 4096, (c)
4.)
5.) , x = -5.04, -0.340, 0.876
6.) Proof
7.)
8.) Proof, x = -1.50, -0.199, 0.668, 5.03
9.) -2.32, -0.593, 0.0930, 0.879, 4.44
Further Uses of DeMoivre’s Theorem
We can use Demoivre’s theorem to write or
as purely real or purely imaginary.
We can do the same for zn+z-n or zn-z-n.
By comparing this with the binomial expansion of these expressions, we can rewrite trigonometric functions raised to a power as trigonometric functions of multiple angles, allowing us to integrate them.
N.B. The above can also be usefully written in exponential form.
Worked Example
Evaluate
Express cos6𝜽 – sin6𝜽 in the form pcosq𝜽 + rcoss𝜽, where p, q, r and s are constants to be determined.
In summary, for your reference, given that and
, then:
Exercise 2

Answers
1.)
2.)
3.) 1
4.)
5.)
6.)
7.)
8.)
Roots of Unity
The Fundamental Theorem of Algebra tells us that equation z3=1 has 3 roots.
We can find these roots by rearranging it into the form z3-1 = 0, noticing that z = 1 is one root, then using this fact to factor z3-1
We could also find them using deMoivre’s theorem.
To do this we rewrite 1 in its general polar form, and then can express the solutions generally as:
(cos(0+2kπ) + isin(0+2kπ))1/3
We apply deMoivre’s theorem to this and then draw the roots on an Argand diagram. Notice that as the angles increase by equal increments, the diagram shows a regular shape.
We can also notice that the roots sum to zero – this can also seen if we represent the three complex numbers as vectors.
This use of deMoivre’s theorem to find roots can be used with any complex number on the right hand side of the equation, not just 1.
Worked Example 1
Find, in exponential form, the 7th roots of unity.
Worked Example 2
Given that z3 – 1 = 0, find the solutions in x + iy form, naming them ,
and
.
Show that the square of one complex root is the other complex root and hence name the three roots ,
,
Hence find the value of .
Worked Example 3
Solve , giving all answers in the form
. Show all your solutions on an Argand diagram.
Exercise 3
1.) Find the 6th roots of unity, giving your answers in integer or exponential form.
2.) The roots of are
,
,
. Determine the value of
.
3.) Find the roots of the equation , giving your answers in exponential form.
4.) Find the 4th roots of -16, giving each root in an exponential form.
5.) A polynomial equation is given as . (a) Show that 1 is one root, then factorise your polynomial into the form (z-1)f(z) = 0, where f(z) is to be stated. (b) Using the four complex solutions, show that
6.) Solve the equation . Show all of these solutions on an Argand diagram.
7.) Find the roots of z12 = -1. Give your answers in exponential form.
8.) Show that
9.) (a) Write down the sixth roots of unity in exponential form, (b) State the two real roots, (c) The polynomial can be written as the product of two linear factors and two quadratic factors. Show that one of the quadratic factors is z2-z+1 and find the other one.
Answers

More advanced problems, including series
Our formulae for z+z-1 and z-z-1 can often help us when tackling problems, by making it easier to write an expression with its real and imaginary parts separated.
Please make careful note that we are now solving purely trigonometric problems, by working with the complex number and then considering real and imaginary parts. This is often the easiest method.
Complex summations
Let’s try and find the value of .
We could start listing out the terms, i.e. , but this doesn’t seem to help.
As is the real part of zn, we can instead consider
, which is a geometric sum equal to
.
Replacing z with , we have
We can multiply through by to give
.
The denominator can now be written as the single term , which will allow us to split the fraction into real and imaginary parts. Writing it out in full gives:
We only need the real part of this fraction, so we have: =
Worked Example 1
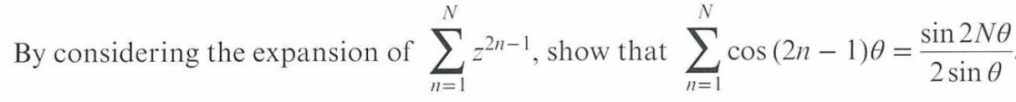
In the following example the denominator is not symmetric, meaning the technique used above to make the denominator whole real or wholly imaginary will not work. In cases where the denominator is of the form , we can multiply thorough by
, utilising the formulae learned above.
Worked Example 2
Find, in any form, the result of
Worked Example 3
Determine the value of
Exercise 4 and General Exercise


Answers

Exercise 4 & Mixed Exercise Worked Solutions
2012 Winter 3 Paper
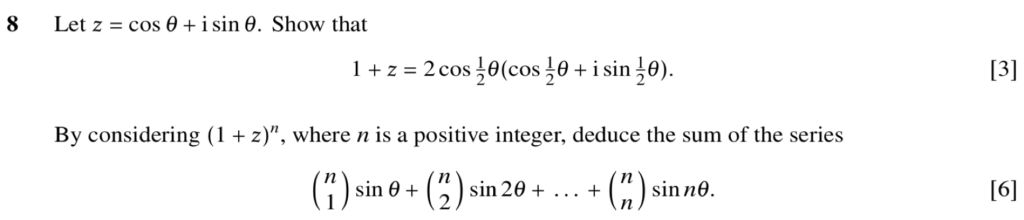
2014 Winter 3 Paper
