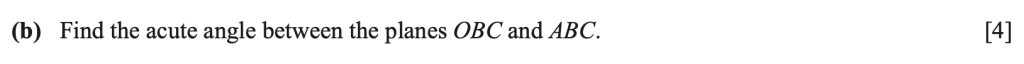We will extend our P3 work on vector equations of lines and the scalar product to start to look at planes and the vector product, and link to the work that we are doing with linear equations and matrices.
Reminder: Scalar product is a.b = |a||b|cos𝜽, where 𝜽 is the angle between the directions of vectors a and b.
Vector Product Rule
The vector product or cross product is calculated as , where
is a unit vector that is a common perpendicular to a and b.
Let us start by calculating n. N.B. the absolute value of this gives us the cross product, i.e. the left hand side of the equation.
The easiest way to calculate the common perpendicular of and
is by calculating the vector determinant,
Worked example
- In each case, find a vector perpendicular to each pair of vectors given:
- -4i + 2j + k and 3i – 7k;
- -2i + 12j – 9k and 4j + 5k;
- i + j + 2k and 2i + 7j -6k.
Now is a unit vector, so by definition has magnitude 1, so the right hand side of the equation,
reduces to absin𝜽 which is the area of a parallelogram, as shown below:

Also, by halving both sides, we get (on the right hand side) magnitude , which is the area of a triangle as shown below:
So, we can conclude that the magnitude of the vector normal to both a and b is actually the area of a parallelogram with sides a and b and that the area of a triangle can be written as
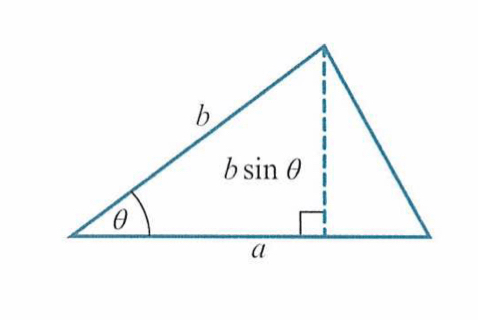
Below we compare using the left had side of the equation and the right hand side of the equation to find the area of a triangle with vertices at 0: (0,0,0), A: (-2,3,6) and B(2,2,1). You will notice that using the left hand side is easier as we don’t need to calculate the angle.
Worked example
Find the area of the triangle ABC, given that the vertices are A: (4, 1, -2), B: (5, 5, 6) and C: (0, 3, 7).
Exercise 1


Exercise 1 Answers

Vector Equation of a Line
- The vector equation of a line is r = a + bt, where
- a is a position vector that goes from the origin to the line; and
- b is the direction vector of the line.
Worked Example
- Find the vector equation of the following lines:
- The line through A and B, where A is (2,3,5) and B is (1,1,2);
- The line through C parallel to the line through A and B, where A is (-1,4,1), B is (0,2,-3) and C is (1,1,5).
Distance from point to line
- Consider foot of perpendicular from point to line; the distance from the point to this point is shortest distance from point to line;
- Calculate the direction vector of the line between the point and the foot, by using a parameter to represent the coordinates of the foot.
- Use scalar product of the directions of these two perpendicular lines (one will include a parameter) to find the coordinates of the foot of perpendicular (by first finding the parameter);
- Once you have found the foot of the perpendicular you can find the distance between the two points using Pythagoras’ Theorem.
Worked Example
Find the shortest distance from point (11, -5, -3) to the line with equation
Worked Example 2
Find the shortest distance between the point P(2,1,4) and the line r = 4i + 4j + 5k + (i + j + k)t
Alternatively (and more easily), we can use the vector product. If we first consider the vector , then the shortest distance from P to the line is |AP|sin𝜽. If we multiply this by the magnitude of the unit vector in the direction of the line |u| it will not change the distance.

So the distance is |AP||u|sin𝜽, which using the vector product we can write as |AP x u|. Note that u is the direction vector divided by its magnitude.
So, in the worked example above, we could calculate AP = -2i-3j–k and u = and calculate the distance using AP x u =
and then taking the magnitude of this, i.e
Worked Example
Find the shortest distance between the point P (3, 2, -1) and the line r = 3j – 4k + (-i +2j – k)t
Shortest Distance between 2 Straight Lines
- Consider two lines:
- r1 = a1 + b1t passing through point P; and
- r2 = a
2+ b2t passing through point Q.
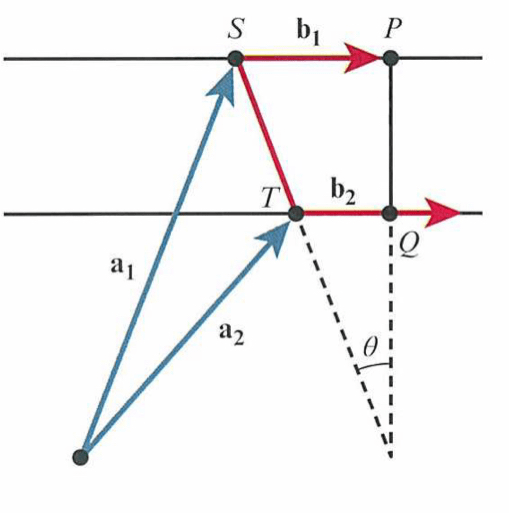
- On the above diagram:
- a1 = OS;
- a2 = OT; and, as it is perpendicular to both lines,
- PQ is parallel to b1 x b2.
We want distance |PQ|, which is equal to |ST|cos𝜽. (1)
Clearly |ST| > |PQ| because |PQ| is the shortest distance between the two lines
Using the scalar product, we note that .
As ST = a2–a1, we can substitute this into (1) and note that the distance is:
e.g. Let and
.
We will find the shortest distance between them.
- a2 – a1 =
- b1 x b2 =
and so |b1 x b2| = √299
Therefore
Worked Example
Find the shortest distance between the lines and
We may need to find the position vectors of P and Q rather than the distance between them.
Consider r1 = and r2 =
If P is on r1, then OP =
If Q is on r2, then OQ =
So PQ = is perpendicular to both direction vectors, i.e.
and
- These two scalar products give us the equations:
- 3s + t = 1; and
- s + 3t = -1,
- which solve to give s = 1/2 and t = -1/2
Hence, and
Worked Example
Points P and Q lie on the lines r1 = 2i + 3j + s(-i+2j+k) and r2 = 3i + j + t(-i+j), respectively, such that PQ is perpendicular to both lines. Find the coordinates of P and Q and the distance between them.
Exercise 2

Answers to Exercise 2

Worked Solutions to Exercise 2
Planes
We can define a plane by referring to its normal,
- Any vector line in the plane AR is necessarily perpendicular to n, so:
- AR . n = 0, so
- (r – a) . n = 0, so
- r.n = a.n. This is the scalar equation of a plane (where a is a known point).
We can use this to get the Cartesian equation of a plane, e.g. if a plane has and we know the point (3,-5,4) on the plane, then
, which tells us that
. In cartesian form this gives x-3y+z = 22.
Se can also use a form which extends the idea used with the vector of a line, and define a plane as r = a + sb + tc, where a is the position vector of a point on the plane and b and c are two non-parallel vectors on the plane. This is the vector equation of a plane.
If we know two non-parallel (direction) vectors on the plane we can easily find the normal by taking the cross product of them.
e.g. If we want to find the equation of the plane passing through A: (2, 1, 2), B: (3, 0, -1) and C: (4, 5, 1) we would take AB = and AC =
, so the vector equation of the plane is
. We could then use this information to find the other two forms of the equation. First we need the normal, n =
=
. We then calculate that a . n =
, so we can conclude that
, from which we read off the Cartesian form as 13x = 5y + 6z = 33.
Worked Example
Given that the plane Π contains the points A:(2, -5, 1), B:(0, 3, 2) and C: (-4, 1, 1), find the equation of the plane in both vector and Cartesian form.
Intersecting Planes
If 2 planes in space intersect, there will be a line of intersection. There are two angles between the planes, an acute angle and an obtuse angle as shown below. They sum to 180º.

The angles between the planes are equal to the angles between the normals, which can be calculated using the scalar product. Note that if n1 . n2 > 0, then 𝝰 is acute, if n1 . n2 = 0, then 𝝰 is 90º (i.e. the planes are at right angles) and if n1 . n2 < 0, then 𝝰 is obtuse.
Worked example
If A is (2,3,1), B is (-4, -2, 5), C is (3, 3, 2) and D is (0, 0, 4), find the acute angle between the planes ABC and ACD.
As the line of intersection is parallel to both planes, it is also perpendicular to both normals. So if the line of intersection is r = a + bt, then b = n1 x n2.
To find the position vector, a, of a line of intersection, we set one of the coordinates in each of the cartesian equations of the planes equal to zero, and solve the remaining equations to find a point on the line of intersection. This works because unless one of the planes is flat on the xy-axis, say, there must be a point on them where the z-coordinate is zero.
Worked Example
Find the vector equation of the line of intersection of the planes x + 3y – z = 1 and 2x + 4y + z = 6.
Lines intersecting planes
Lines will either be fully on planes, parallel to them, or intersect them at a point.
To find the point of intersection, write the equation of the line in parametric form, then substitute this into the plane’s equation to find the value of the parameter.
- e.g. suppose:
- plane is P: 3x + 4y -5z =22; and
- line is
- So the equation of the line in parametric form is:
- x = 2 – t,
- y = 1 + t; and
- z = 4 – 3t.
- Substituting this into the cartesian equation of the plane gives 3(2-t) + 4(1+t) – 5(4-3t) = 22, or -10 +16t = 22, so t = 2.
- Substituting this back into the equation of the line gives the point of intersection as (0,3,-2)
If the plane and line don’t meet, we can identify if they are parallel or if the line is on the plane.
- If the scalar product of the direction vector of the line and the normal of the plane gives a result of zero, then we know that the line is parallel to or on the plane.
- If the line is actually on the plane, then when we substitute the equation of the line in parametric form into the cartesian equation of the plane, we will find that it is true for all values of the parameter.
- If it isn’t on the plane, then when we substitute the equation of the line in parametric form into the cartesian equation of the plane, we will find that it is true for no values of the parameter
Worked Example
Show that the line r = i – j + 8k + (2i – k) t lies in the plane x + 5y + 2z = 12
The two angles (one acute and one obtuse) between a line (that isn’t parallel to a plane) and a plane can be determined using the scalar product of the normal of the plane and the direction vector of the line.
Worked Example
Find the angle between the line r = 8i – 3j + k + (2i + 2j – k)t and the plane 3x-y=2
Shortest distance between a point and a plane
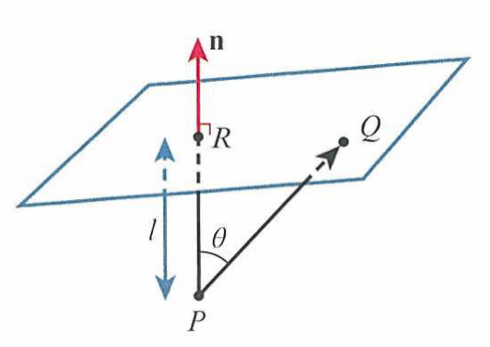
Form a line parallel to the normal passing through the point (i.e. PR above). Write the equation of the line in parametric form and substitute it into the equation of the plane to find where it meets the plane. This gives us the coordinates of point R. We can then find the distance PR (e.g. by Pythagoras’).
Worked example
Find the shortest distance between the point (1,2,3) and the plane 4x + y – z = 12
Exercise 3 & General Exercise

General Exercise

Answers to Exercise 3 and General Exercise


Worked Solutions to Exercise 3
Relevant Past Paper Question
Summer 2020 Paper 11:



Summer 2020 Paper 11 Mark Scheme
Summer 2020 Paper 13:
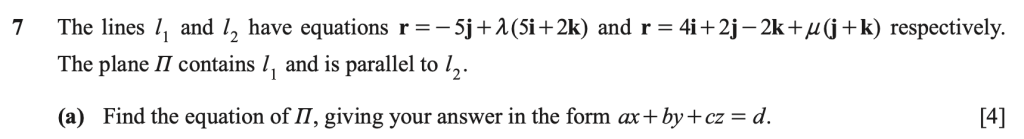


Summer 2020 Paper 13 Mark Scheme
Winter 2020 Paper 11:



Winter 2020 Paper 11 Mark Scheme
Winter 2020 Paper 12: