An object of mass m moving with velocity v has momentum P = mv, a vector quantity.
For an object to change its momentum, a force must be applied. If it is applied over time, then and so
. Assuming that mass doesn’t change over time, this simplifies to
.
As a force is required to change momentum, we can look at Newton’s second law. Integrating it gives:
As and the velocities at the times given are u and v, so we have
, which becomes
. From this we have that Ft = mv – mu, which we call impulse, equal to the change in momentum. Impulse is not explicitly tested in the 9231 syllabus.
Conservation of momentum
The law of conservation of momentum states that when two particles collide, m1u1 + m2u2 = m1v1 + m2v2.
We use “before & after” diagrams to solve problems. Consider for instance a particle of mass 2kg travelling on a smooth horizontal surface with velocity 5ms-1 that collides with a second particle of mass 1kg that was at rest. We say the particles coalesce if they then move together as a single particle. We can use a before & after diagram and the conservation of momentum formula to find what speed the coalesced particle moves at.
Kinetic energy
If two particles collide, we can compare the inital KE and final KE to find out how much energy is lost. If the collision is perfectly elastic, conservation of energy tells us that the initial KE and the final KE are equal.
When particles coalesce on impact, we call them inelastic.
Let’s consider two perfectly elastic particles of mass m travelling with velocities 2u and u, as shown below:

and
So conservation of energy gives us the equation 5u2 = v12 + v22 to solve. We aren’t going to solve this today, as we need further techniques to establish the are many different solutions to it.
We are also going to use Newton’s Experimental Law, also known as Newton’s Law of Restitution.
This tells us that there is a constant called the coefficient of restitution, e = (speed of separation) ÷ (speed of approach), which is between 0 and 1 and tells us the elasticity of the particles.
e = 0 is perfect inelasticity, so the particles will coalesce, and e = 1 is perfect elasticity.
So in our above example, we have , where the numerator show us how quickly the second particle gets away from the first one, and the denominator shows us how quickly the particles approach.
So, in our example, and so v2 – v1 = u.
From conservation of momentum we have that 2mu + mu = mv1 + mv2, giving us 3u = v1 + v2. Combining these two equations gives us that v1 = u and v2 = 2u.
Worked Example 1
Two particles, P and Q, are travelling on a smooth horizontal plane. P has mass 3kg and Q has mass 1kg. P has velocity 3u and Q has velocity u. P then collides with Q in a perfectly elastic collision. Find the velocity of each particle after the collision. Confirm that the kinetic energy is the same before and after the collision.
Worked Example 2
Two smooth spheres of equal radius are resting on a smooth surface. Sphere A has mass 2m and sphere B has mass 3m. The coefficient of restitution between the spheres is 2/3. Sphere A is projected towards B with velocity 2u and sphere B is projected towards A with velocity u. Find the velocity of each sphere after the collision. Find also the loss in kinetic energy.
Worked Example 3
Two smooth spheres of equal radius are resting on a smooth surface. Sphere P has mass m and sphere Q has mass 2m. The coefficient of restitution between the spheres is e. Sphere P is projected towards Q with velocity u. Find a condition on e such that P’s direction is changed.
Exercise 1

Answers

Momentum Exercise 1 Worked Solutions
Oblique Collisions
Now let’s consider a particle travelling towards a wall with velocity u and an angle of 𝜽, as pictured below. Any such situation where the path is not perpendicular to the wall, we call oblique:

As you see on the diagram, we can split the velocity into the component parallel to the wall, uy and the component perpendicular to the wall, ux.
When the particle bounces off the wall, uy is unaffected by the collision, however ux will be subject to the conservation of momuntum.
Once it has bounced off the wall, the component ux will become -eux.
For our second example, we will consider a particle travelling with velocity 2u, directed at an angle of 30º to a wall, with coefficient of restitution 1/2 between the particle and the wall, as pictured below (with 𝛼 = 30º). We want to find the velocity of the particle after the collision.
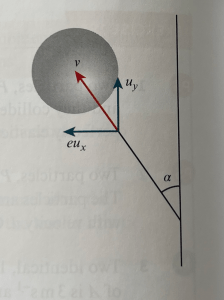
We have uy = 2ucos(30) = u√3 and ux = 2usin(30) = u.
Once the particle has bounced off the wall, -eux = -u/2.
So the overall velocity afterwards is , which is
ms-1.
We can also find the angle that the particle makes with the wall afterwards, using , which gives 𝛼 = 16.1º.
Worked Example 4
A particle is projected along a smooth horizontal surface with velocity u. The particle collides with a smooth vertical wall at an angle of 60º. Given that the coefficient of restitution between the particle and the wall is 0.3, find the angle between the wall and the path of the particle after the collision.
Worked Example 5
A particle of mass 3kg is travelling on a smooth horizontal surface with velocity 4ms-1. The particle collides obliquely with a smooth vertical wall with coefficient of restitution 1/3. Given that the angle between the path of the particle and the wall before the collision is 40º, find the loss in kinetic energy due to the collision.
Worked Example 6
When a smooth sphere travelling on smooth horizontal ground collides obliquely with a smooth vertical wall, it rebounds off the wall at right angles to its original direction. If the sphere is travelling with velocity u and its path makes an angle of 60º with the wall before the collision, find e, the coefficient of restitution.
Multiple collisions
Consider two particles with masses m and 2m resting on a smooth horizontal surface. Particle A is projected towards B with velocity u. A strikes B and then B will go on to strike a smooth vertical wall, rebounding at 90º. If the coefficient of restitution between the particles is 7/8 and the coefficient between B and the wall is 1/3, we will try to show that there are no further collisions.
We will need two diagrams. One for the collision of A and B and one for the collision of B with the wall. The collision of A with B is shown below:

Conservation of momentum gives mu = mv1 + 2mv2, so u = v1 + 2v2.
Newton’s experimental law gives , so
Adding these equations gives us that and
. So we know that A travels in the opposite direction, away from the wall.
B hits the wall and as shown below it bounces off with velocity and is now travelling in the same direction as A.
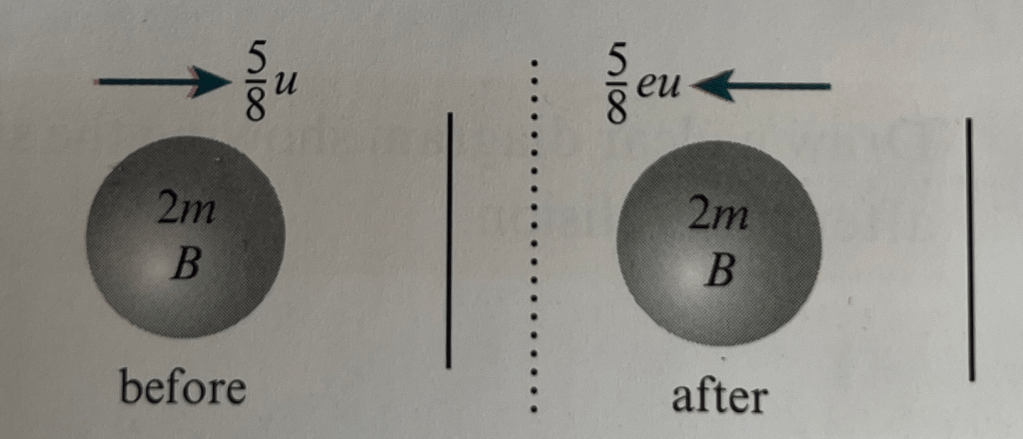
As , so B will never catch up with A and there will be no more collisions.
Worked Example 7
Two smooth spheres, P and Q, of masses 2m and 3m, respectively, are resting on a smooth, horizontal surface. Sphere P is projected towards Q with velocity 2u. P strikes Q and Q begins to travel towards a smooth vertical wall. The coefficient of restitution between the spheres is e. Q strikes the wall at right angles and rebounds off the wall, where the coefficient of restitution between Q and the wall is 1/8. Given that P’s direction is reversed, and that Q strikes P again, find the range of values of e.
Three Particles
Let’s now consider three spheres. They are of equal size on a smooth horizontal surface. A has mass m, B has mass 2m and C has mass m. The coefficient of restitution between A and B is 1/3, whereas between B and C it is 2/3.
A is projected towards B with velocity u, as shown below:

Conservation of momentum gives mu = mv1 + 2mv2, from which we get u = v1 + 2v2.
Newton’s experimental law gives , from which we get
.
Combining these gives and
.
We can then draw a second diagram to consider B and C colliding:

Here conservation of momentum gives us and so
.
Newton’s experimental law gives , leading to
Combining these gives and
.
As B’s velocity is now greater than A’s velocity there will be no further collisions.
We can now work out the loss in kinetic energy. Initial KE was and final KE is
. So the loss in kinetic energy is
Joules .
Worked Example 8
Three particles, P, Q and R, have respective masses 2kg, 3kg and 1kg. All rest on a smooth horizontal surface. P is projected towards Q with velocity 5ms-1. At the same time Q is projected towards P with velocity 1ms-1. Given that P, Q and R are all in the same line and that the coefficient of restitution between all the spheres is 0.6, find the speed of R after it is hit by Q.
Oblique Collisions
In an oblique collision between two particles it is important to note the line of centres between the two objects. When they collide we consider (a) the conservation of momentum along the line of centres and (b) the conservation of momentum perpendicular to the line of centres.
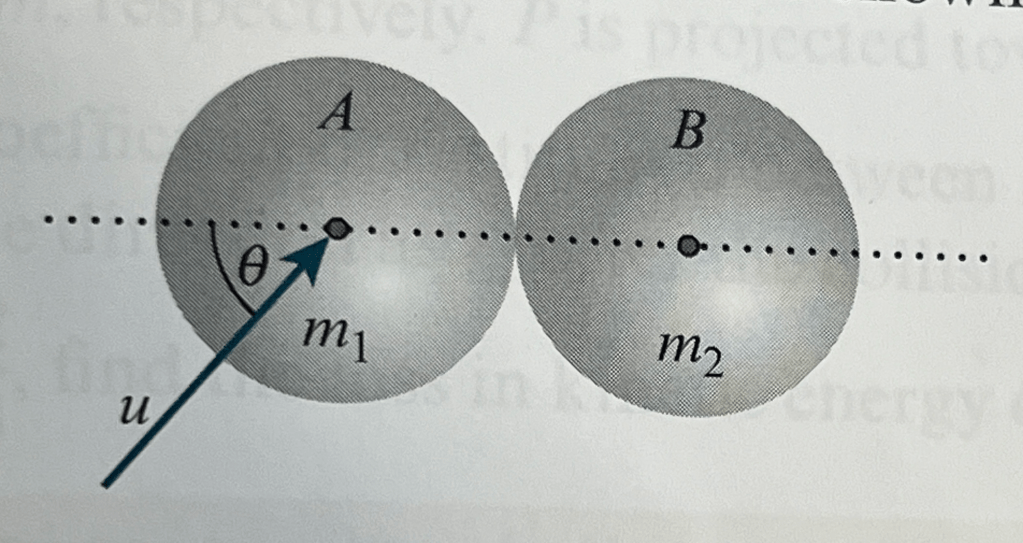
Consider A with mass 2m and B with mass 2m, both with equal radii, resting on a smooth horizontal surface. B is initially at rest and A is projected with speed u towards B. When they collide, the direction of A is at 45º to the line through the centres of A and B.
Given that the coefficient of restitution between the particles is 1/2, we will find the speeds of the particles after colliding.

First we consider the components of the speed of A. The only component affecting the collision is ux. Note that ux = ucos(45) and uy = usin(45).
Using conservation of momentum we find that the vertical components cancel to give 2mucos(45) = 2mv1 + 2mv2, which we can write as u√2 = 2v1+v2.
Newton’s experimental law gives which can be written as
. Combining these leads to
and
. So the speed of sphere B after the collision is
ms-1 .
A’s final speed is given by =
. Hence the speed is
ms-1.
We can also determine the angle of deflection caused by the collision. This is the angle that shows the change in direction travelled before and after the collision. The direction relative to the line through the centres is 45º, then after the collision the angle is . This gives an angle of tan-1(2) = 63.4º, so the angle of deflection is 63.4º – 45º = 18.4º.
Worked Example 9
Two smooth spheres of equal radii, P and Q, are at rest on a smooth horizontal surface. The coefficient of restitution between them is 1/4. Sphere P has mass m and sphere Q has mass 3m. Sphere P is given an initial speed of 4u and is projected in a direction that will collide with Q. Given that the angle between the direction of P and the line through the centres of P and Q at the point of impact is 60º, find the angle of deflection for P.
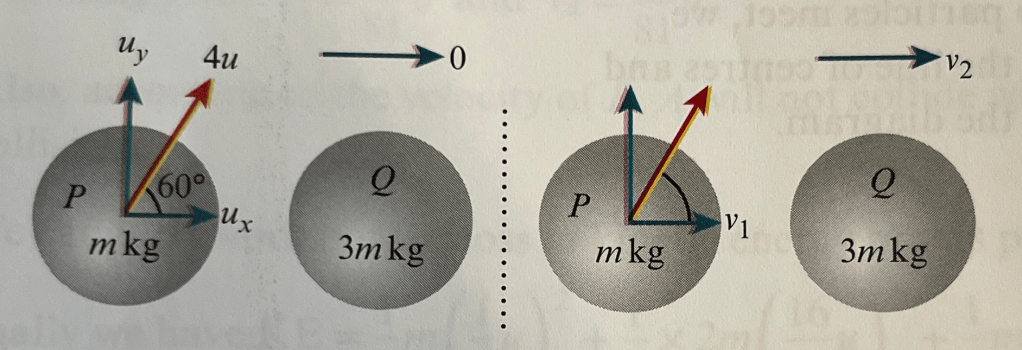
Exercise 2


Momentum Exercise 2 Worked Solutions
Mixed Exercise

Answers to Both Exercises