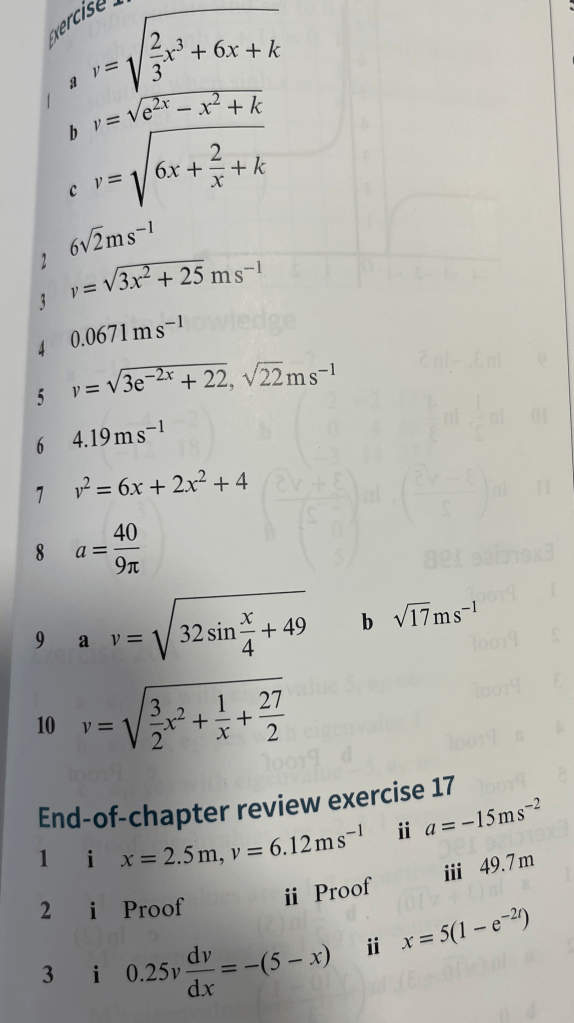9231. FM. Linear Motion under a Variable Force

Up until now we have treated air resistance on falling objects as negligible. In reality, it is a variable force proportional to the speed of the object that impacts the acceleration of the object.

Objects influenced by a variable force will experience variable acceleration. We will model these either by using differential equations, such as $\frac{dv}{dt} = f(t)$ and $v \frac{dv}{dx} = g(x)$ , or by giving displacement or velocity as functions of time.

Acceleration is defined as the rate of change in velocity over time, and velocity is defined as the rate of change in displacement over time, so we have $a = \frac{dv}{dt} = \frac{d^2 x}{dt^2}$ .

So, if we know that a particle is travelling in a straight line with variable acceleration a = -2t ms^-2 and initial velocity 4ms^-1, we can integrate acceleration to get v = -t² + c. As the initial velocity is 4 (i.e. v=4 when t=0, we get 4 = 0 + c, so c is 4 and v = -t² + 4, giving velocity as a function of time.

Worked Example 1

A particle is travelling in a straight line with a = sin(2t) ms^-2. It passes through the point O with speed v = 9/2 ms^-1 at time t = 0s. Find:

(a.) v in terms of t ;

(b.) the displacement, x, in terms of t, relative to the point O.

Obviously, we can relate acceleration to the force acting on a particle, using NII. If a particle of mass 2kg has a force of 2t² N acting on it, we can calculate its velocity as a function of time.

NII gives us $2t^2 = 2 \frac{dv}{dt}$ , and so $\frac{dv}{dt} = t^2$ . Integrating gives $v = \frac{1}{3} t^3 + c$ . If we knew the initial conditions, we could determine c.

Worked Example 2

A particle of mass 4kg is travelling in a straight line under the influence of a single opposing force. This force has magnitude e^0.5tN. If the particle passes through a point O at time t = 0s with velocity 2ms^-1, find expressions for both velocity and displacement in terms of t.

We can also use velocity functions to determine acceleration functions, by using differentiation.

Worked Example 3

A particle is travelling along a straight path such that its displacement at time t is given by the expression x = 2ln(t²+1) – 2 m. Find the time when the velocity is at a maximum.

Remembering that displacement is represented by the area under a velocity time graph, we can use definite integration to calculate velocity.

Worked Example 4

A particle is travelling along a straight line such that v = (t³ – t² + 2)ms^-1. Find:

(a) The acceleration when t = 2;

(b) The distance travelled during the third second.

Exercise 1

Answers to Exercise 1

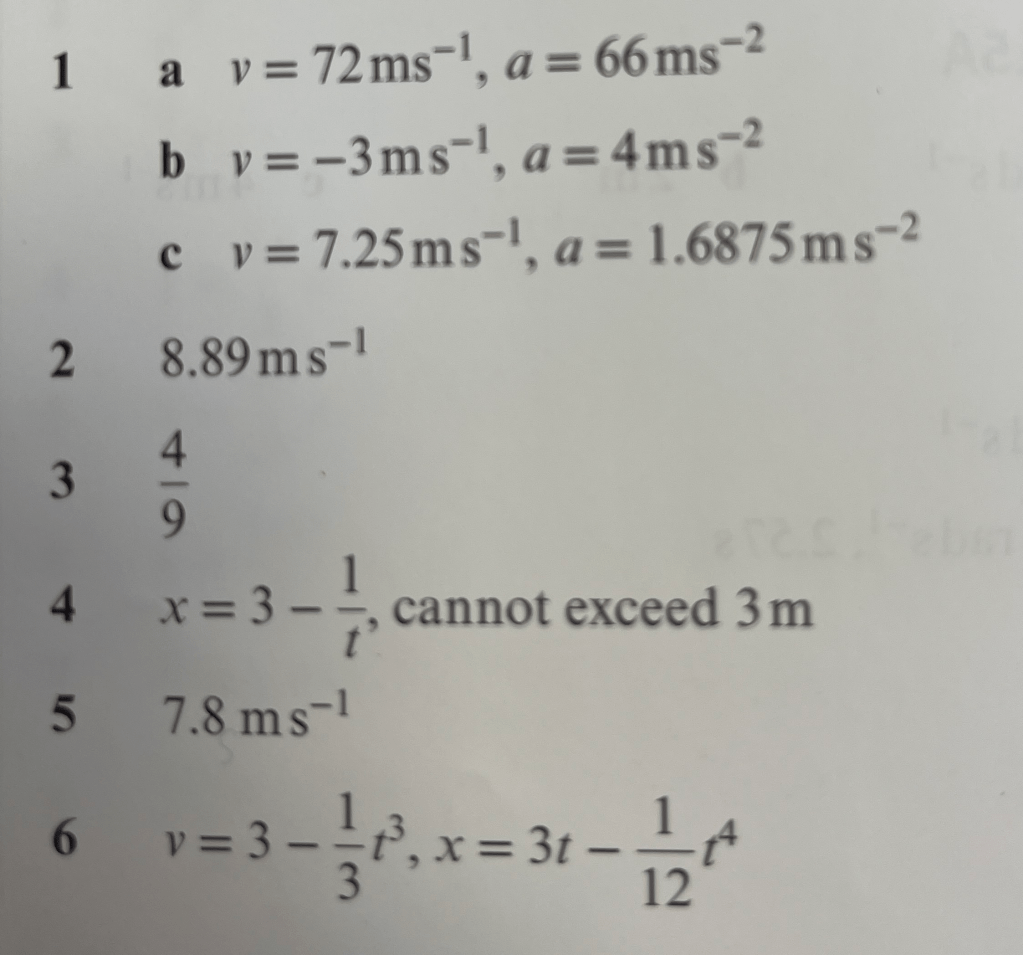
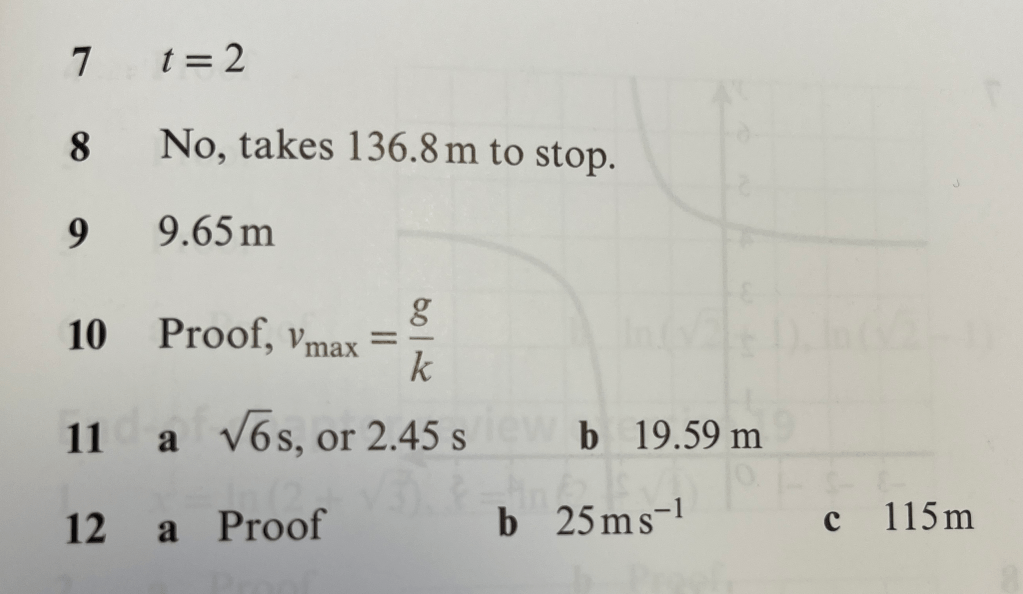
Variable Motion Exercise 1 Worked Solutions

Acceleration with respect to Displacement

Consider a particle moving with acceleration given as $a = - \frac{2}{x^2} ms^{-2}$ where v = 2ms^-1 when x = 1m. To solve it we need to set up a differential equation.
We can’t use the equation $\frac{dv}{dt} = - \frac{2}{x^2}$ as the variables don’t match.

Using the chain rule $\frac{dv}{dt} = \frac{dv}{dx} \times \frac{dx}{dt}$ however we can write $v \frac{dv}{dx} = \frac{-2}{x^2}$ .

We can then separate the variables to give $\int v dv = - \int \frac{2}{x^2} dx$ . Integrating this gives $\frac{1}{2} v^2 = \frac{2}{x} + c$ and the initial conditions show that c = 0 and so $v = \frac{2}{ \sqrt{x} } ms^{-1}$ .

Summary – In general to solve differential equations involving acceleration and displacement, we use acceleration in the form $a = v \frac{dv}{dx}$

Worked Example 1

A particle is travelling in direction Ox away from the point O with acceleration a = 2(x-1)²ms^-2. Given that the velocity is 4ms^-1 when x = 1m, find the veloicty when x = 4m.

Worked Example 2

A particle is subject to forces that produce an acceleration of a = -tan(x) ms^-2, where 0 ≤ x ≤ π/3. The particle travels in a straight line, and when x = 0m it passes through the point O with velocity 4ms^-1.

(a.) Describe what happens to this particle after passing through O;

(b.) Find the velocity of the particle in terms of the displacement;

(c.) Find v when $x = \frac{ \pi }{3} m$

Worked Example 3

A particle is moving along the x-axis such that its acceleration is of magnitude 2x ms^-2 for 0 ≤ x ≤ k. The particle passes through the point O where x = 0m, and at this point v = 12ms^-1. Given that the acceleration is directed towards O, find:

(a.) The velocity of the particle when x = 4m;

(b.) The value of k.

Again, we can use Newton’s second law if a force is applied.

Worked Example 4

A toy car of mass 0.5kg is travelling in a straight line and passes through point O with velocity 8 ms^-1. Then an opposing force of magnitude $\frac{4}{x+1} N$ acts on the car, where x is measured from point O. Find: