Maximum and Minimum Values

The graph of a quadratic function is always parabolic, which means it will have a minimum or a maximum point. It will also have a vertical line of symmetry, which will pass through this minimum or maximum point. If the graph cross the x-axis, then this line of symmetry will be halfway between the two points where it intersects this axis.

Worked Example 1  a.) Plot the graph of y = x2 – 4x – 5 for values of x from -2 to +6; b.) Identify the values of x where the curve intersects the horizontal axis; c.) Hence find the coordinates of the maximum or minimum point.

Drawing a graph each time you want to find a maximum or a minimum point takes a long time though. Instead, we can use algebra. We will look now at how factorising can help us with this (by indicating first where the graph crosses the x-axis.

Worked Example 2 Find the coordinates of the turning point of the curve y = x2 + x – 6.  State whether the turning point is a maximum or a minimum value.

Worked Example 3 For the curve with equation 6 – x – 2x2, a.) Will the turning point of the curve be a maximum or a minimum? Give a reason for your answer; b.) Write down the coordinates of the turning point; c.) State the equation of the line of symmetry.

Of course, not all quadratic equations factorise. Graphically, this is because not all quadratic equations cross the x-axis. In these cases we can use the completing the square method. We’ve probably seen this before, but let’s practice it here.

Worked Example 4 a.) Write x2 – 8x + 18 in completed square form; b.) State whether y = x2 – 8x + 18 has a maximum or a minimum. c.) Sketch this curve.

Worked Example 5 Use the method of completing the square to work out the coordinates of the turning point of the quadratic function f(x) = 2x2 – 8x + 9

Sometimes you will be asked to sketch a graph of y = f(x) for a specific interval of values of x, i.e. for a restricted domain. The corresponding set of y-values are the range.

Worked Example 6 The domain of the function y = 6x2 + x – 2 is -3 ≤ x ≤ 3. Sketch the graph and find the range of the function.

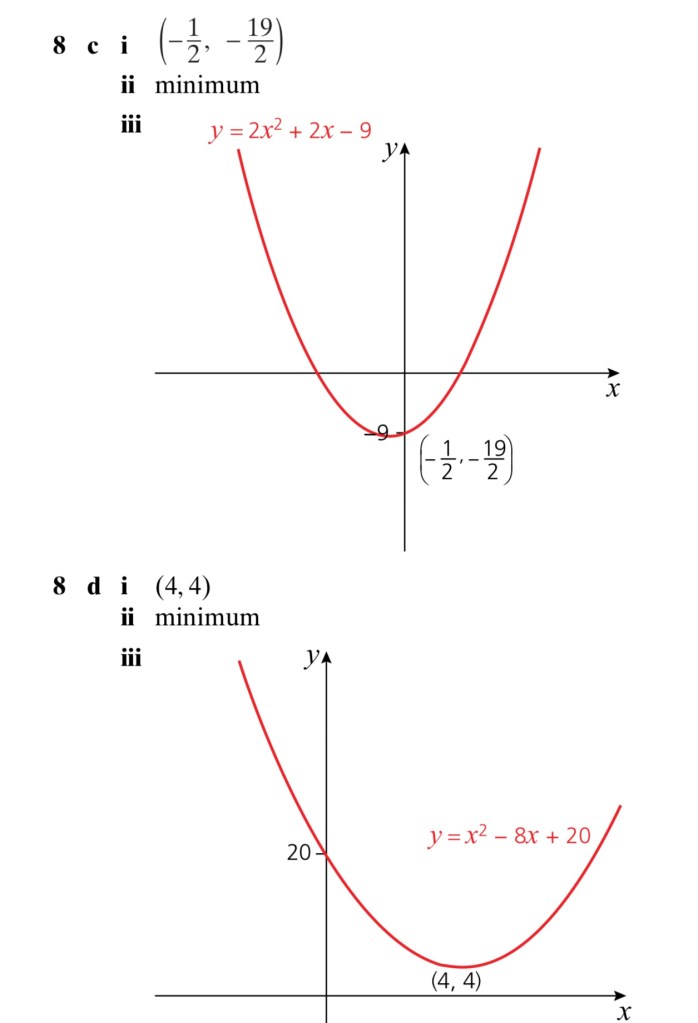
Exercise 1

Answers to Exercise 1

Quadratic Formula

Roots of a quadratic equation are represented graphically by the points where the parabola crosses the x-axis. We can see graphically that a quadratic equation may have two, one or zero roots.

We can use the completing the square method to find roots and by using algebra and the completing the square method we can find a general solution for quadratic equations.

Worked Example 7 a.) Solve 2x2 + x – 4 = 0 b.) Solve ax2 + bx + c = 0

The solution to (b) in the worked example above is known as the quadratic formula, which is so widely applied that I should be memorised.

Within the quadratic formula, the part b²-4ac is known as the discriminant because it helps us identify how many roots there are.

Worked Example 8 a.) Show that 4x2 – 12x + 9 = 0 has a single root by: (i) factorising; (ii) inspecting the discriminant;  b.) How many roots do the following equations have: (i) 4x2 – 12x + 8 = 0 (ii) 4x2 – 12x + 10 = 0 (c) Show that the equation 3x2 – 2x + 4 = 0 has no real solution.

Intersection of lines and curves

So far we’ve only been looking at where the parabolas intersect the x-axis. We can easily generalise this to consider where the parabolas intersect other lines.

Worked Example 9 a.) Find the coordinates of the points of intersection of the line y = 4 – 2x and the curve y = x2 + x;  b.) Sketch the line and the curve on the same axes.

Worked Example 10 a.) Use algebra to show that the line y = 6x – 19 touches the curve y = x2 – 2x – 3 and find the coordinates of the point of contact; b.) Sketch the line and curve on the same axes.

Worked Example 11 a.) Sketch the graphs of the line y = x – 3 and the curve y = x2 – 2x on the same axes; b.) Use algebra to prove that the line and curve don’t meet.

Solving problems using quadratic equations

Worked Example 12 A triangle has a base of (2x+1) cm, a height of x cm and an area of 68 cm2. a.) Show that x satisfies the equation 2x2 + x – 136 = 0; b.) Solve the equation and work out the base length of the triangle.

Solving quadratic inequalities

Here we will only consider quadratic inequalities that factorise. The method to find the solution interval is to first calculate the roots and then inspect each of the intervals separated by the roots to consider whether they will be positive or negative. We will apply this method in the worked example below:

Worked Example 13 Solve these quadratic inequalities a.) x2 – 2x – 3 < 0 b.) x2 – 2x – 3 ≥ 0

Worked Example 14 Solve 2x + x2 > 3

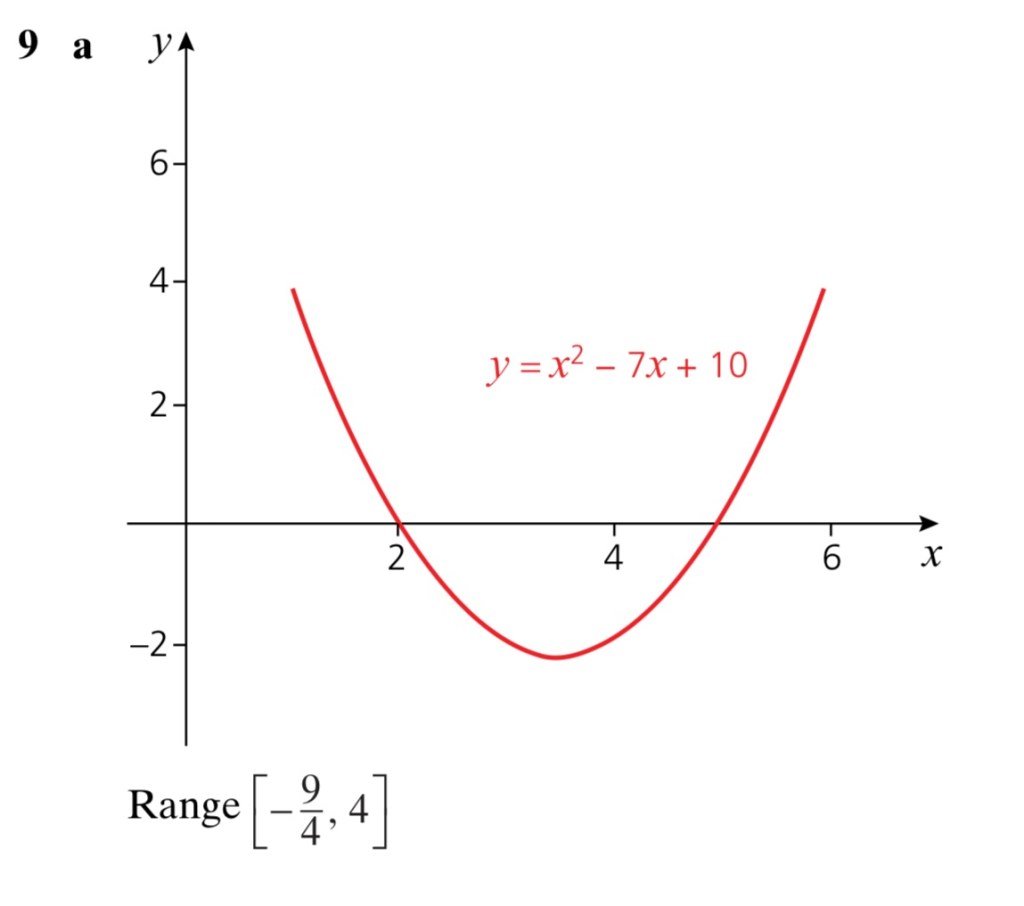
Exercise 2

Answers to Exercise 2