FUNCTIONS SECTION 1 – DOMAIN, RANGE AND INVERSE FUNCTIONS
Function
A function is a rule that associates each element of one set (the input) with only one element of a second set (the output).
It is possible for more than one input to have the same output.
Functions Notation
We can use the notation f(x) = 3x – 5 or the notation f:x|->3x-5
Domain
The domain of a function f(x) is the set of all possible inputs. This is the set of values of x that the function operates on. If no domain is given, it is assumed to be all real values of x, often denoted by ℝ.
Range
The range of the function f(x) is all the possible output values, i.e. the
corresponding values of f(x)
Worked Example 1. Mapping Diagram
(1.) For the function , draw a mapping diagram to show the outputs for the set of inputs “all prime numbers from 1 to 20”.
(2.) For the same function, draw a mapping diagram to show the outputs for the set of inputs “all even numbers between 1 and 10 (inclusive)”
(3.) What number is not in the domain of this function (i.e. cannot be an input).
Mappings
Mapping is a more general concept than function. We can talk about it as a process of taking an object to its image. We can consider 4 types of mapping:
One – One: Every object has a unique image and every image comes from only one object.
Many – One: Every object has a unique image but at least one image comes from more than one object.
One – Many: At least one object has more than one image but every image comes from only one object.
Many – Many: At least one object has more than one image and at least one image comes from more than one object.
Types of Function
In order to be a function, a mapping must be either one-one or many-one.
Worked Example 2.
Sketch each function and say whether it is one-one or many-one:
a.) y = x + 3
b.) y = x2 – 1
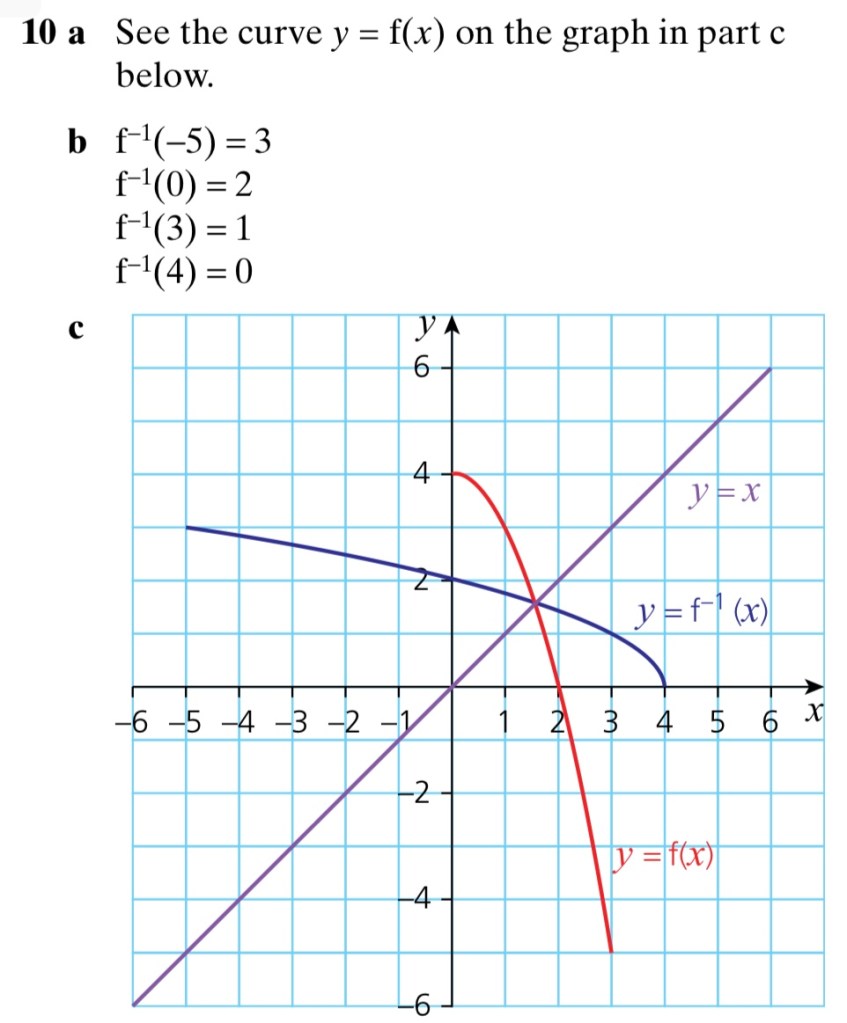
Inverse Functions
An inverse function undoes the effect of the function. e.g. “Multiply by two” is the inverse of “Divide by two”.
All one-one functions have an inverse, but many-one functions do not.
Worked Example 3
a.) Use a flow chart to find the inverse of the function:
b.) Sketch the graphs of y=f(x) and y=f-1(x) on the same axes. Use the same scale on both axes.
c.) What do you notice?
Worked Example 4
a.) Find g-1(x) when g(x) = x/3 + 4
b.) Sketch y = g(x) and y = g-1(x) on the same axes. Use the same scale on both axes.
Worked Example 5
a.) Sketch the graph of the function f(x) = x2 for -4 ≤ x ≤ 4;
b.) Explain, using an example, why f(x) does not have an inverse with -4 ≤ x ≤ 4 as its domain;
c.) Suggest a suitable domain for f(x) so that an inverse can be found.
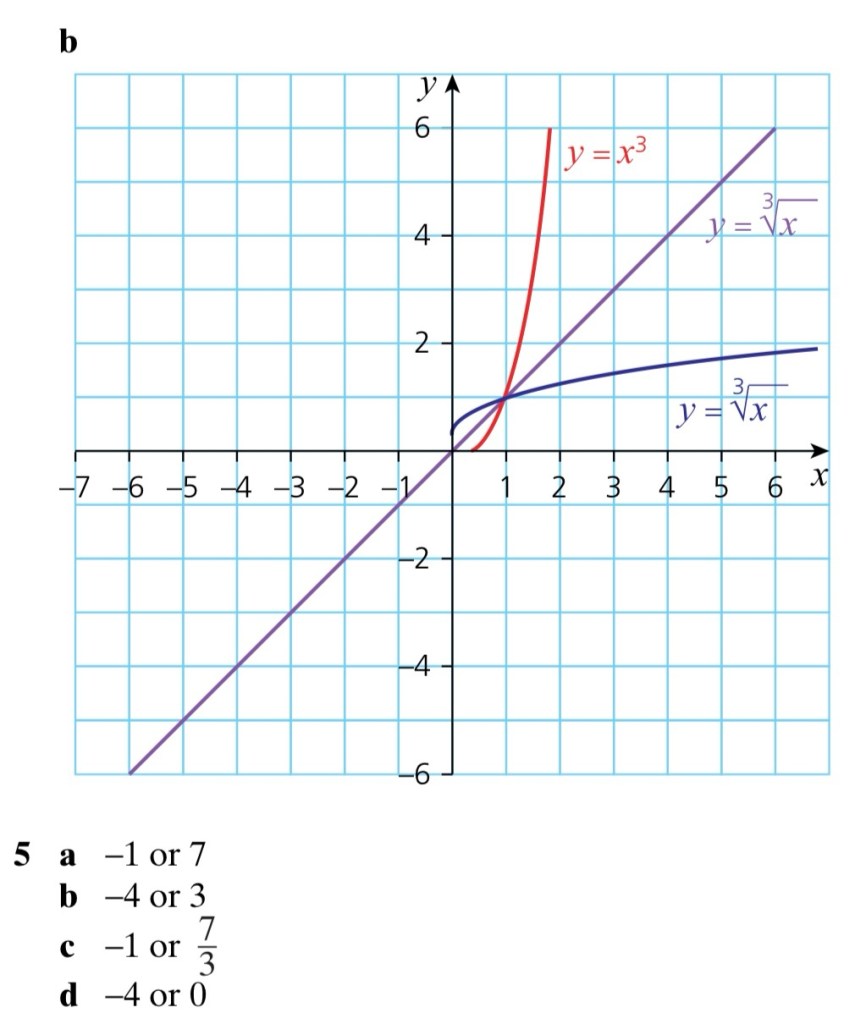
Exercise 1. Domain, Range & Inverse Functions


Answers



FUNCTIONS SECTION 2 – COMPOSITION OF FUNCTIONS & MODULUS FUNCTION
Composition of Functions
Applying one function and then another is called composition of functions.
For example, if f(x) = 6x – 4 and g(x) = 3x + 2, then the composite function fg(x) = 6(3x + 2) – 4, so fg(x) = 18x + 8.
Note that gf(x) involves composition in a different order and is not the same as fg(x). Let’s check this.
Note that to calculate gf(x), we need the range of f(x) to be within the domain of g(x). Similarly to calculate fg(x) we need the range of g(x) to be within the domain of f(x).
means f(f(x)), so the function f is applied twice.
Worked Example 1. Composition of Functions
Given that f(x) = 2x, and
, find:
(a.) fg(x) (b.) gf(x) (c.) . (d.) fgh(x) (e.) hgf(x)
Worked Example 2. Composition of Inverse Functions
(a.) Find when
(b.) Find
(c.) Find
(d.) What do you notice?
Worked Example 3. Composition of Trigonometric Functions
Using the functions f(x) = sin(x) and , express the following as functions of x: (a) fg(x) (b) gf(x) (c)
Modulus Function
The modulus of a number is its positive value, regardless of whether the number is positive or negative, sometimes called its magnitude or absolute value. For example, |-13| = 13. Also, |13| = 13.
Note that |x| = x when x ≥ 0 and that |x| = -x when x<0.
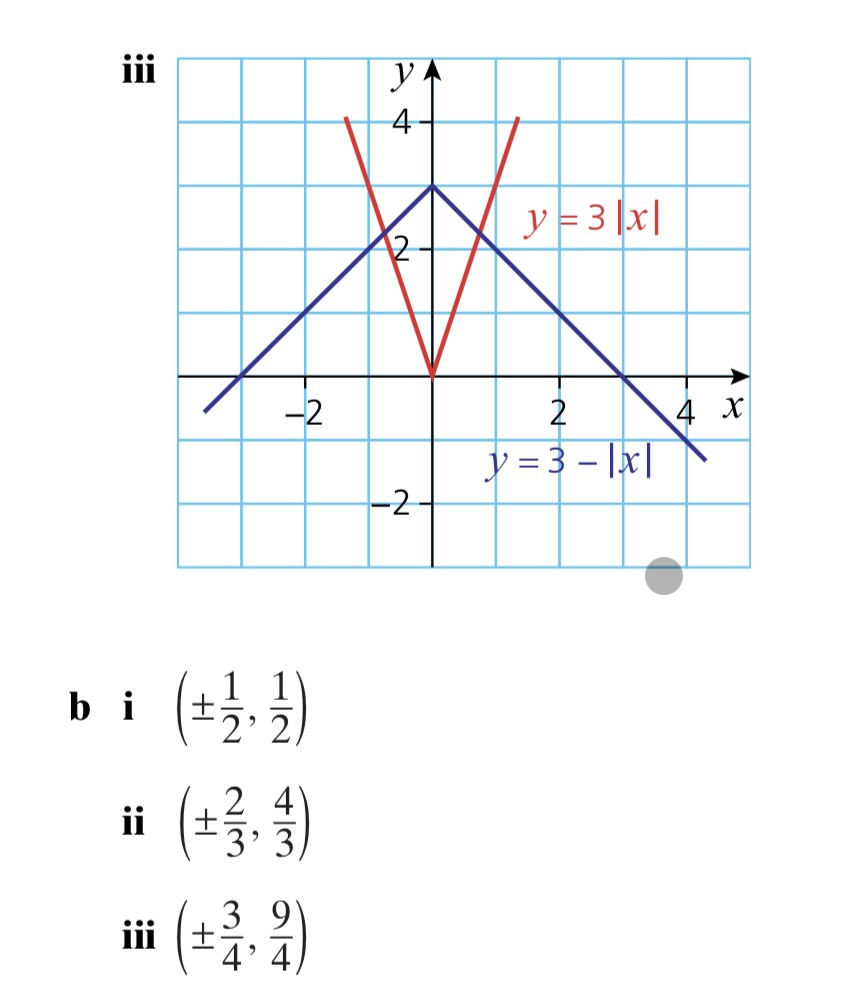
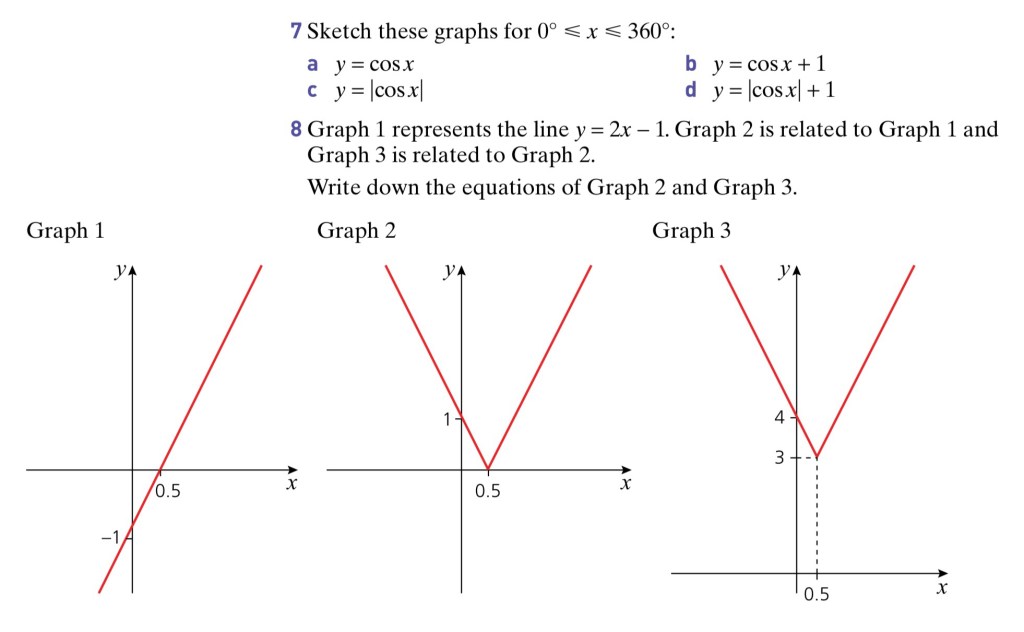
So a graph of the modulus function is simply a graph of the underlying function, with any parts below the x-axis reflected in the x-axis.
Worked Example 4. Sketching Modulus Functions
For each of the following, sketch y = f(x) and y = |f(x)| on separate axes:
(a) y = x – 2, for -2 ≤ x < 6
(b) , for -3 ≤ x ≤ 3
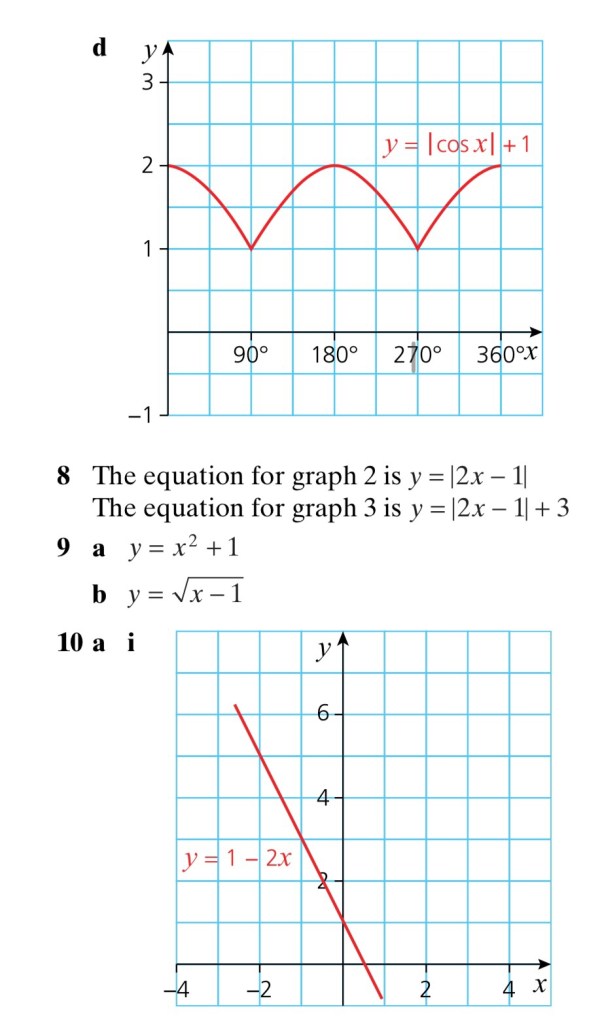
(c) y = cosx, for 0º ≤ x ≤ 180º
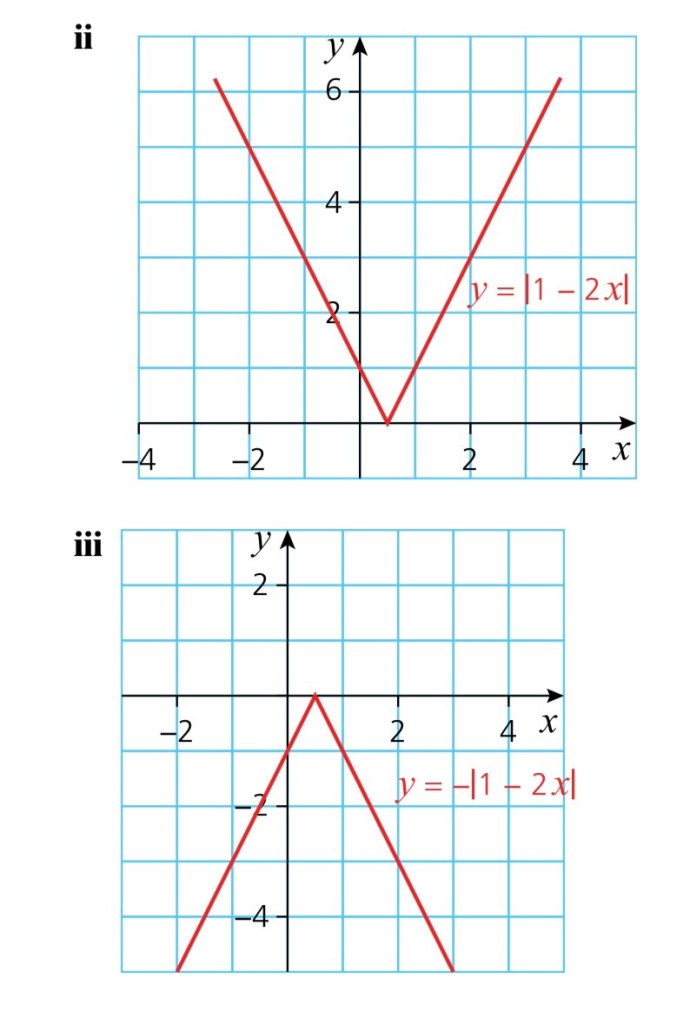
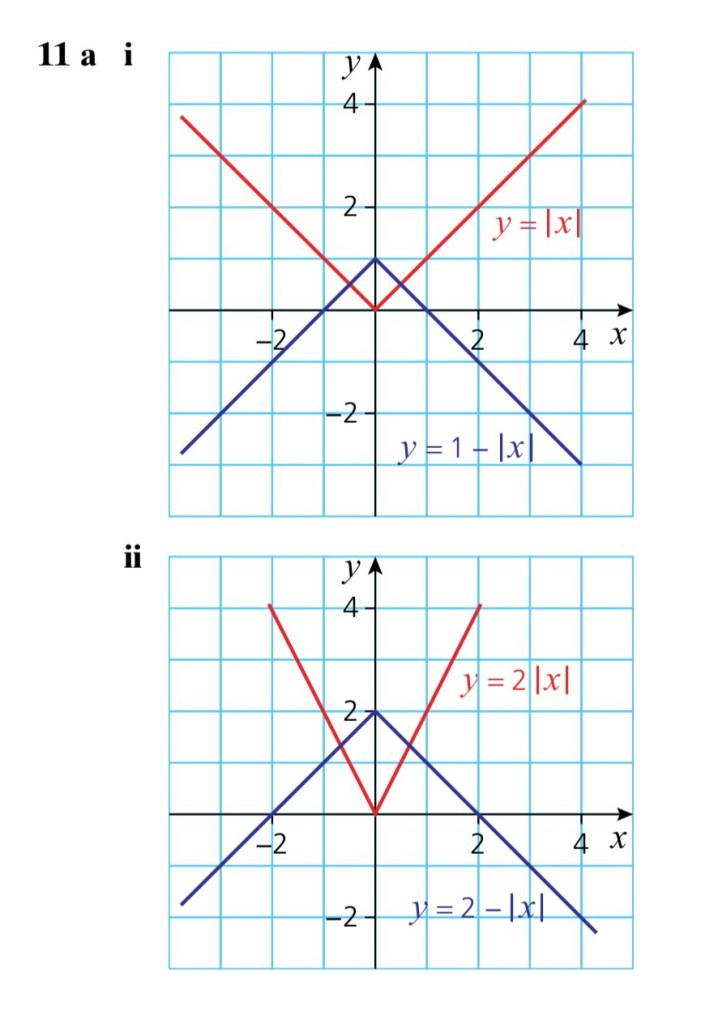
Exercise 2. Composition of Functions & Modulus Function



Answers