Multiplying and dividing polynomials

There are several methods for multiplying and dividing polynomials. In the worked examples below we will multiply by expanding brackets and we will divide by comparing coefficients, but if you know alternate methods you are welcome to use those instead in the following exercise.

Worked Example 1 Multiply (x2 – 5x + 2) by (2x2 – x + 1)

Worked Example 2 Divide (x3 – x2 – 2x + 8) by (x+2)

Exercise 1

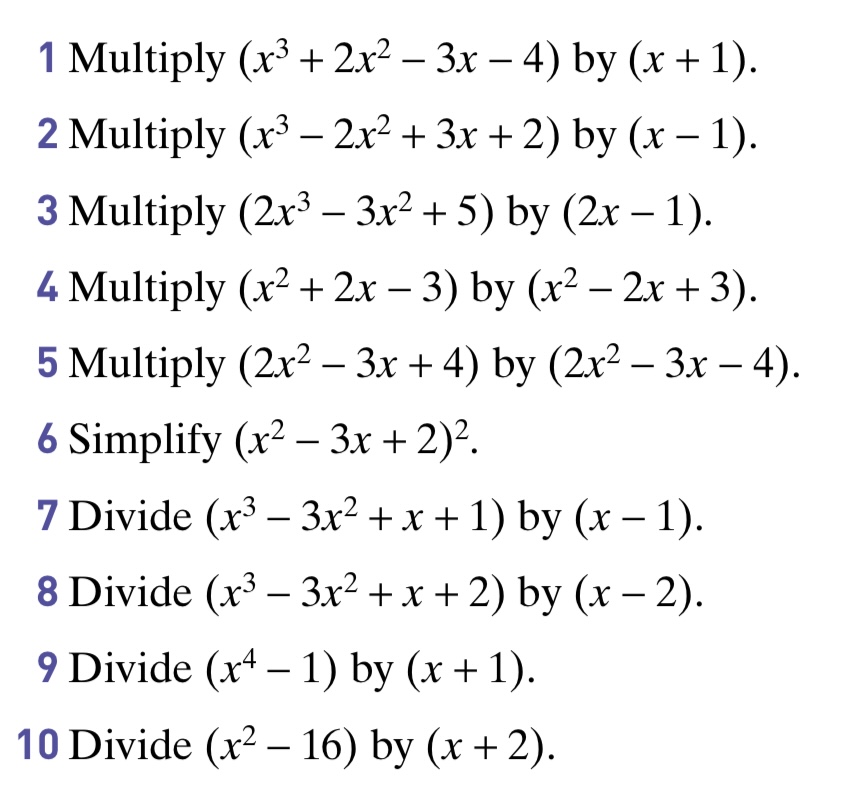
Answers to Exercise 1

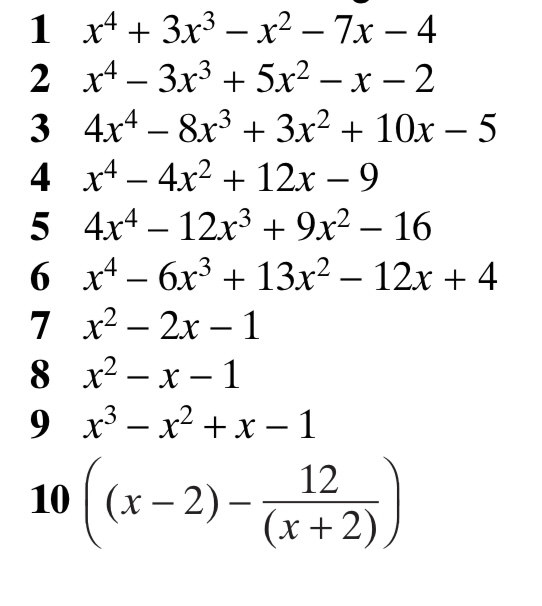
Solving Cubic Equations

Factorising an equation allows us to identify its roots, that is the points where it crosses the x-axis.

Worked Example 3 a.) Draw the graph of y = x3 – 5x2 + 2x + 8, by plotting values of x from -2 through to 5; b.) Hence solve the equation x3 – 5x2 + 2x + 8 = 0

Sometimes, although a graph won’t identify all the roots, it will identify one or two, and the others can be identified, either by using trial and improvement, or by using polynomial division.

Worked Example 4 Draw the graph of y = 2x3 – 7x2 + 2x + 3 and hence solve the equation 2x3 – 7x2 + 2x + 3 = 0

Factor Theorem

Not all polynomials can be factorised, however when they can be factorised, we can solve them immediately by reading the roots from the factors. This can be expressed in the Factor Theorem.

Factor Theorem If (x − a) is a factor of f(x), then; f(a) = 0, and; x = a is a root of the equation f(x) = 0.

The converse of the factor theorem also holds true (and is often the more useful form).

When testing integer values using the Factor Theorem, we only need to test factors of the constant in the polynomial.

Worked Example 5 a.) Show that x = 2 is a root of the equation x3 – 3x2 – 4x + 12 = 0 and hence solve the equation; b.) Sketch the graph of y = x3 – 3x2 – 4x + 12

Worked Example 6 Given that f(x) = x3 – x2 – 4x + 12, a.) Show that (x-3) is a factor of f(x); and b.) Solve the equation f(x) = 0.

Let’s combine these skills for a more complete example:

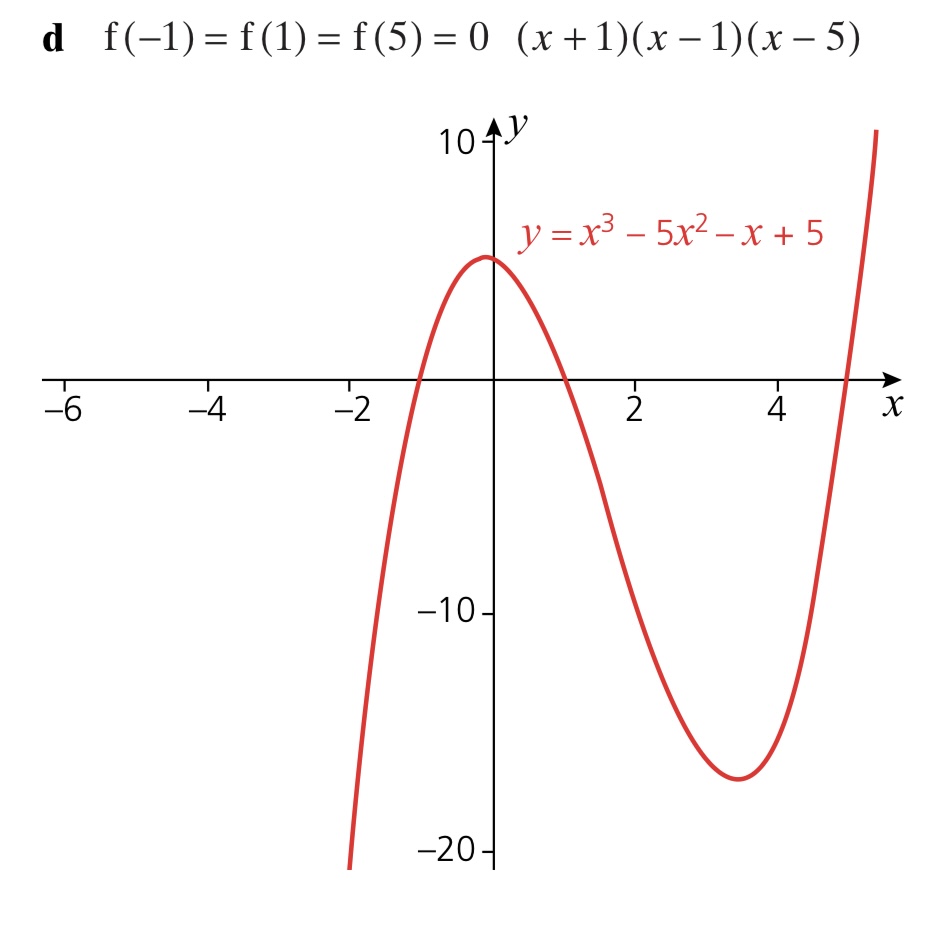
Worked Example 7 a.) Work systematically to find a linear factor of x3 – 5x2 – 2x + 24; b.) Solve the equation x3 – 5x2 – 2x + 24; c.) Sketch the graph of x3 – 5x2 – 2x + 24; d.) Sketch |x3 – 5x2 – 2x + 24| on a separate set of axes.

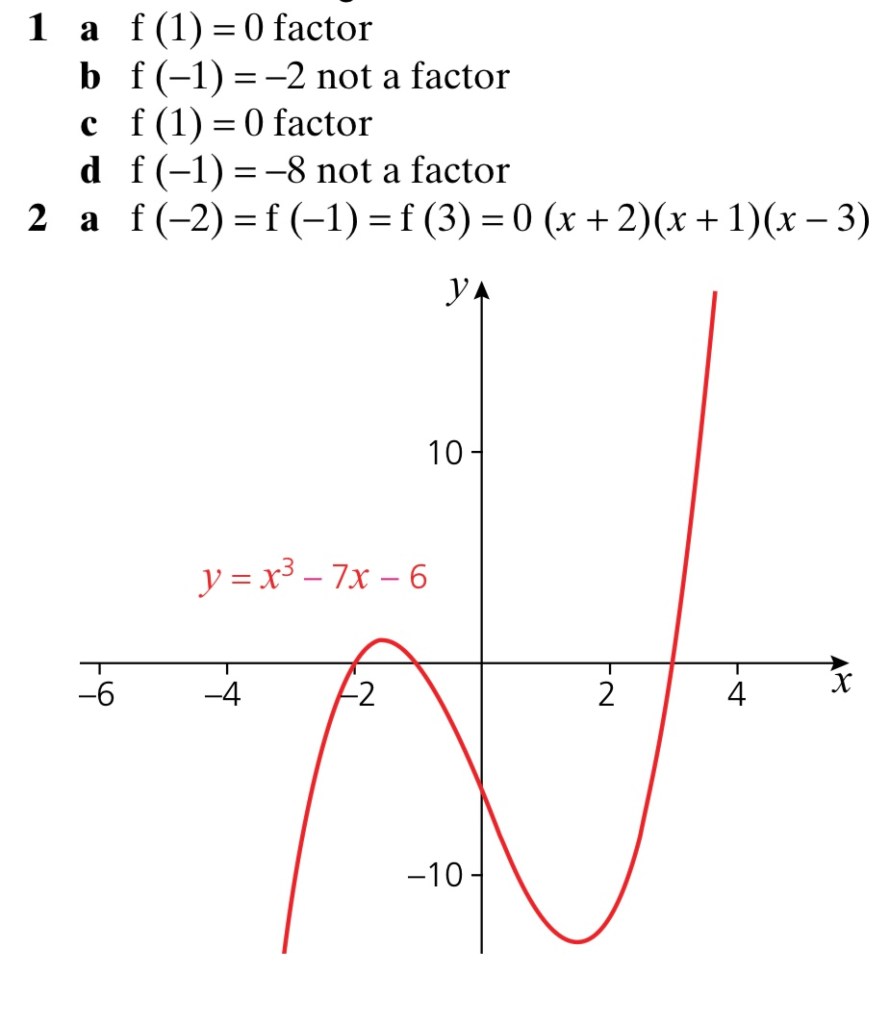
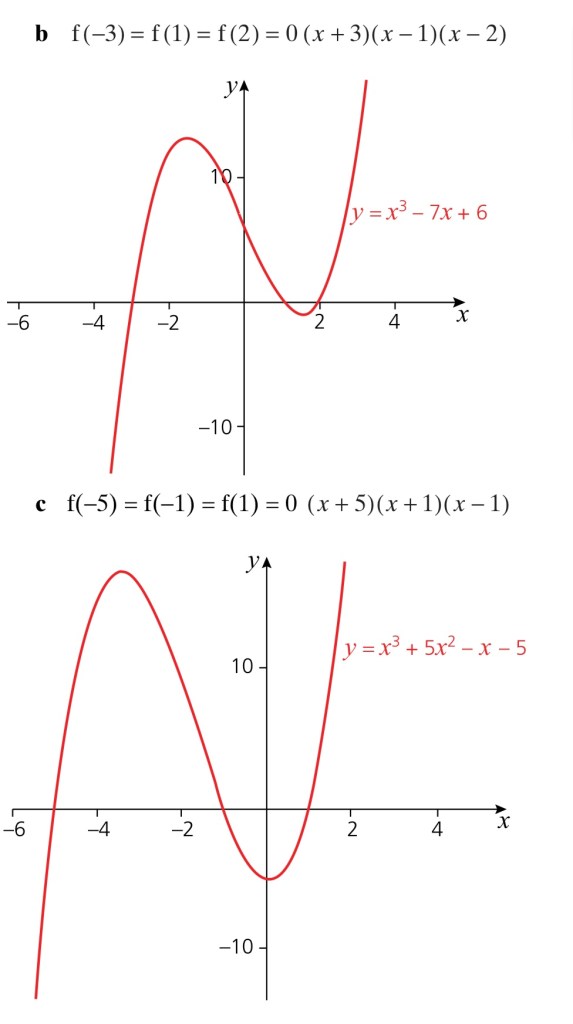
Exercise 2

Answers to Exercise 2

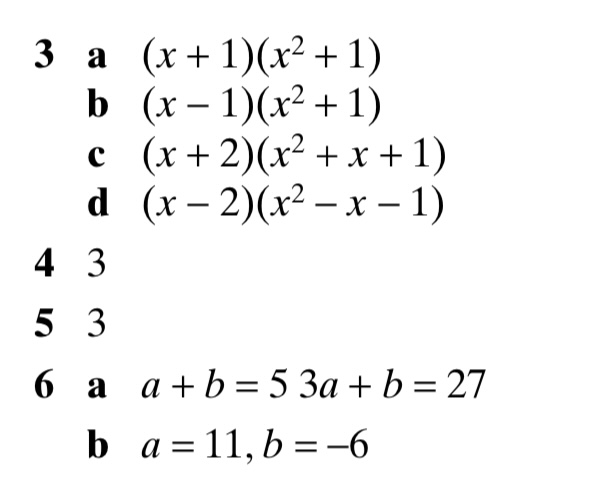
Remainder Theorem

TBC