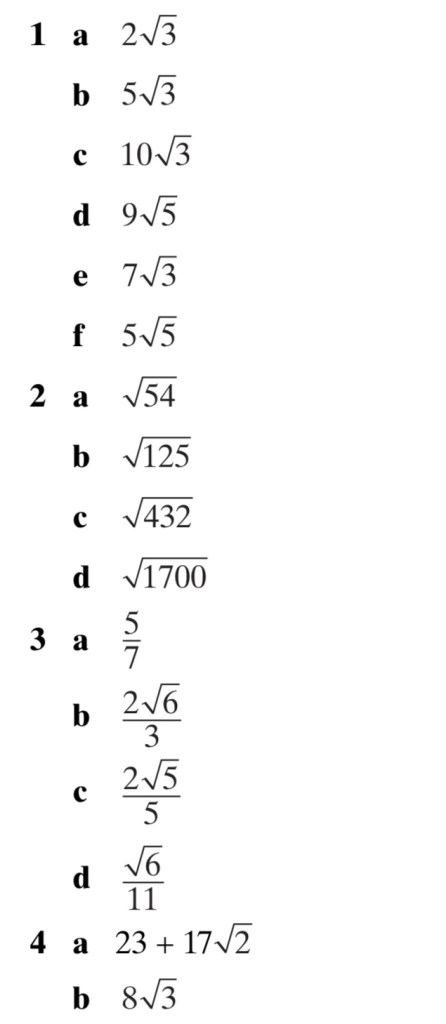We should be familiar with the following index rules:

a^m x aⁿ = a^m+n

a^m ÷ aⁿ = a^m-n

(a^m)ⁿ = a^mn

a⁰ = 1

a^-1 = $\frac {1}{a} $

Worked Example 1 a.) Write as a fraction.

Fractional Indices

If instead of writing , we write 3ⁿ x 3ⁿ = 3, we notice that 3²ⁿ = 3, so n = 1/2. This demonstrates that .

In general, .

We can combine this with what we already know to give the more general

Worked Example 2 Calculate

Worked Example 3 Simplify the following, leaving your answers in standard form: a.) (5 x 105) x (4 x 102) b.) (8 x 105) x (4 x 102)

Exercise 1

Surds

Surds are irrational numbers such as or . We often choose to work with surds in their exact form, rather than representing them with rounded decimal numbers.

To simplify a surd, we must check for any square numbers within the root and write them outside of the root, as in the next example:

Worked Example 4 Simplify

Worked Example 5 Simplify

We add and subtract surds by treating them as like terms.

Expanding brackets involving surds follows the same principles as expanding brackets in general.

Worked Example 6 Simplify

Worked Example 7 Simplify

Worked Example 8 Simplify

Worked Example 9 Simplify

Rationalising the Deonominator

It is better to present fractions within surds on the numerator and not the denominator. If we wish to remove them from the denominator, we simply need to multiply the fraction through by the surd.

Worked Example 10 Simplify

Worked Example 11 Simplify

Worked Example 12 A right angled triangle has shorter sides of lengths ( )cm and ( )cm. Work out the length of the hypotenuse.

Worked Example 13 A ladder of length 6m is placed 2m from a vertical wall at the side of a house. How far up the wall does the ladder reach? (Leave your answer as a surd)

Exercise 2

Exercise 2 Answers