Modulus Functions and Graphs

The modulus or absolute value of a number is its positive size, regardless of whether it is positive or negative. So |2| = 2 and also |-2| = 2.

Worked Example 1 a.) Set up a table for the graphs y = x+2 and y = |x+2| for -6≤x≤2. b.) Draw both graphs on the same axes.

Worked Example 2 Solve the equation |2x+3| = 5 a.) Graphically;  b.) Algebraically.

Worked Example 3 Solve the equation |2x+5| = |x-4|

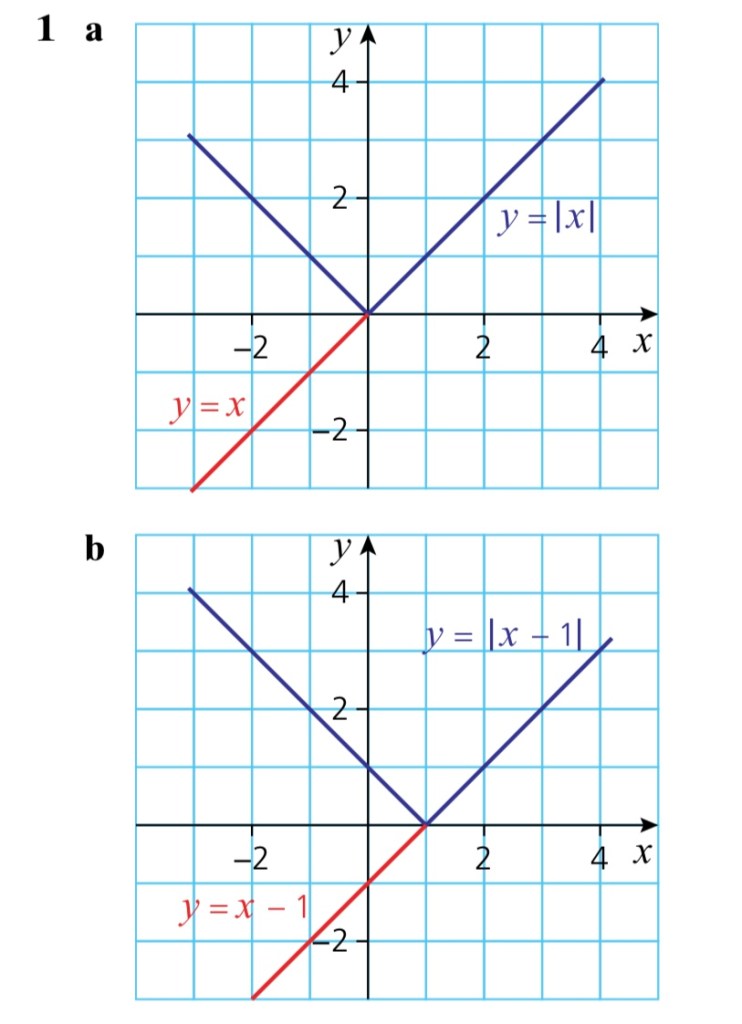
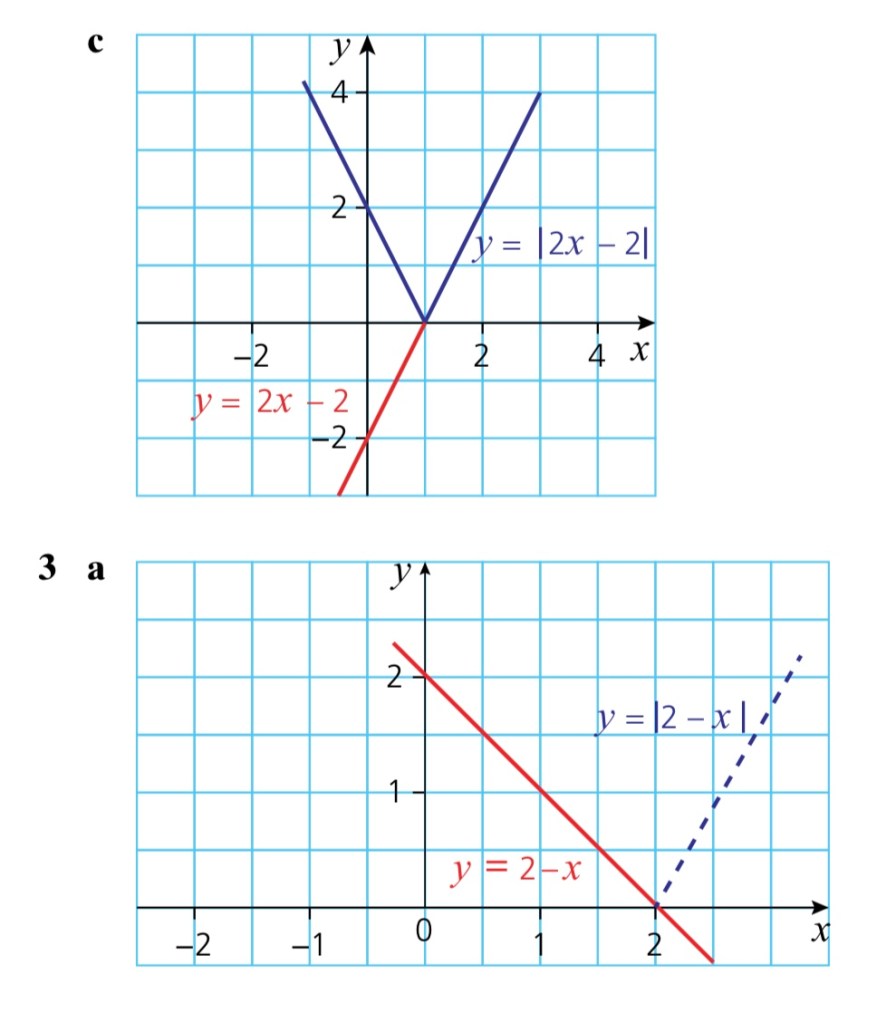
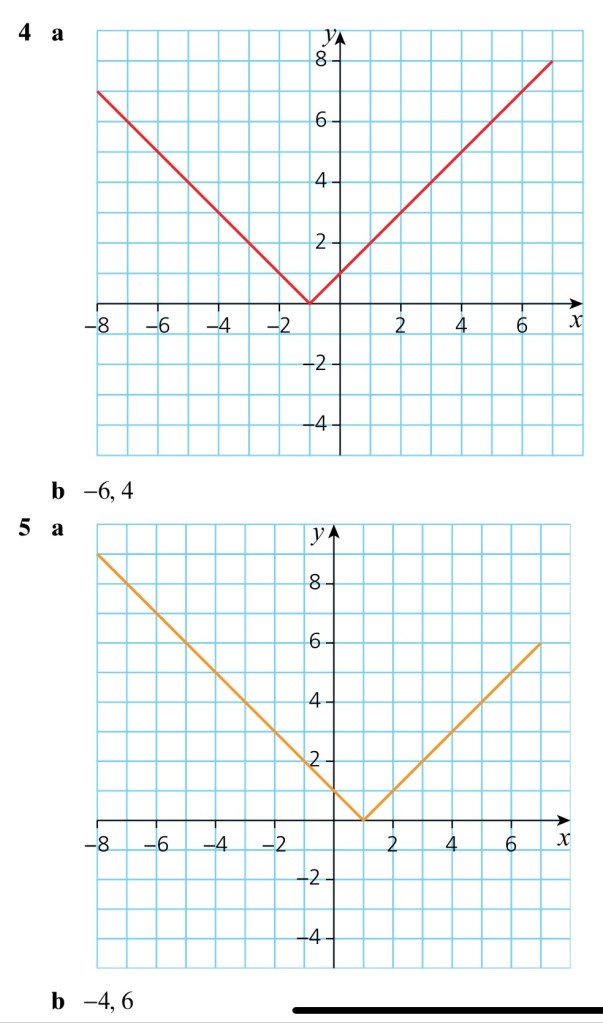
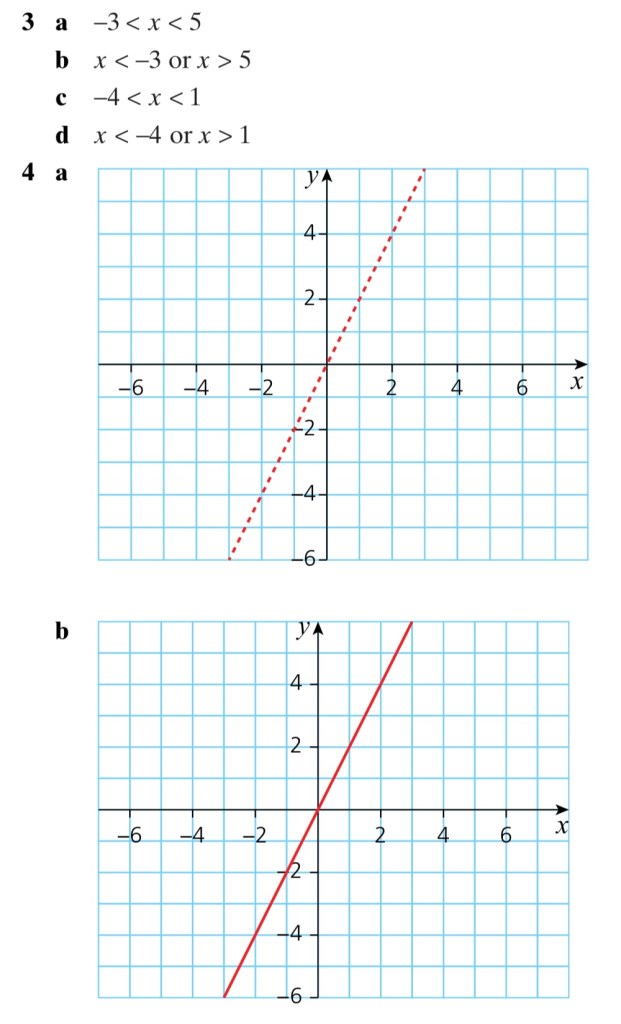
Exercise 1

Answers to Exercise 1

Solving Modulus Inequalities

With inequalities in one variable, we can use number lines to represent their solutions, following the appropriate strict vs. non-strict conventions.

Worked Example 4 a.) Solve algebraically the inequality |x-3|>2;  b.) Illustrate the solution on a number line.

Worked Example 5 Write the inequality -3 ≤ x ≤ 9 in the form |x-a| ≤ b and show a and b on a number line.

Worked Example 6 Solve the inequality |3x+2| ≤ |2x-3|

Worked Example 7 Solve the inequality |x+7| < |4x|

In 2-dimensions we use regions instead of lines to represent inequalities. We also have a solid vs dotted line convention for non-strict vs strict inequalities.

Worked Example 8 Illustrate the inequality 3y – 2x ≥ 0 on a graph.

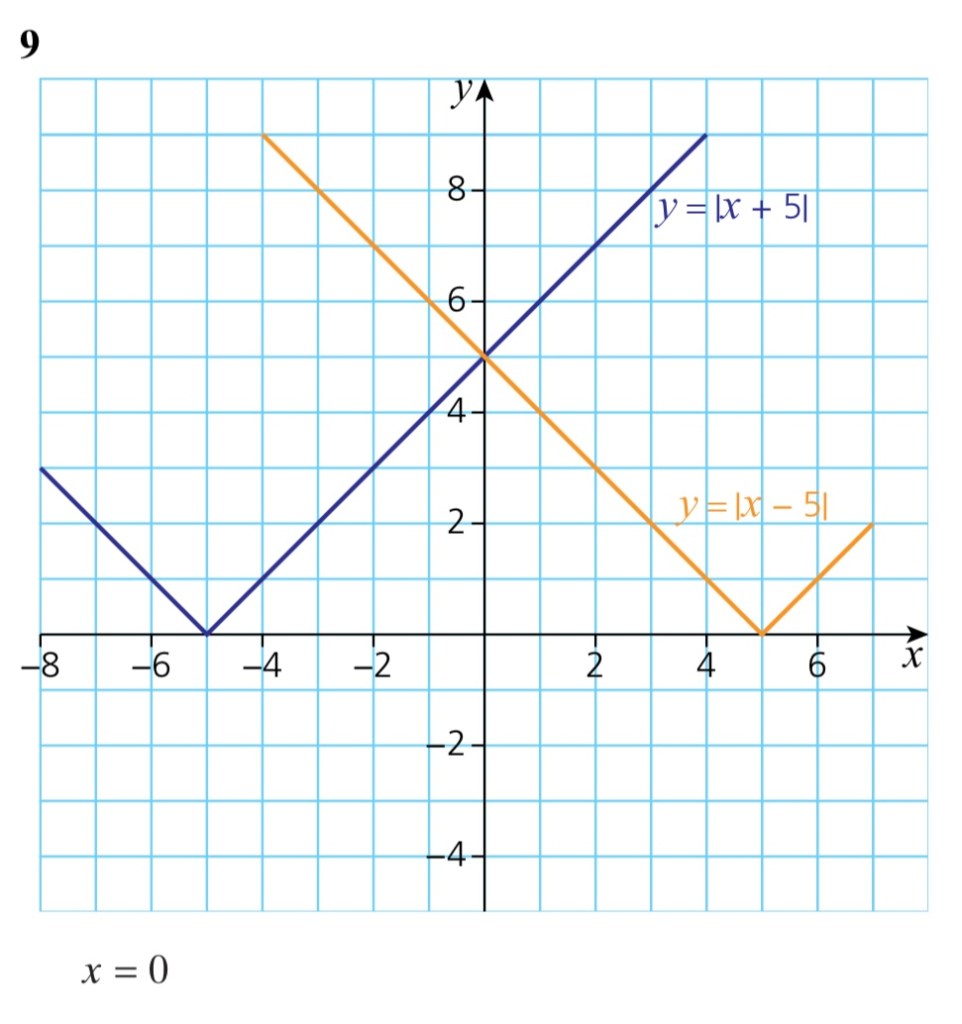
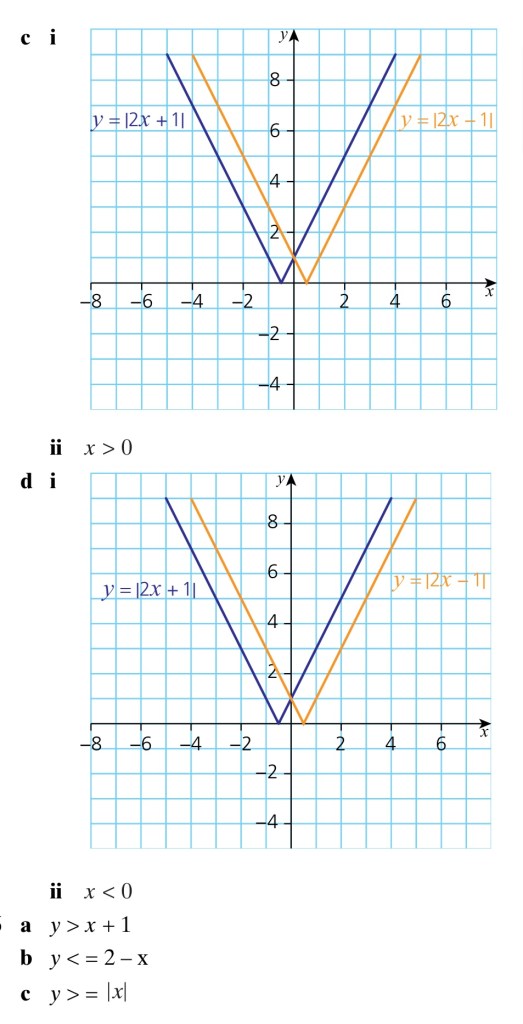
Exercise 2

Exercise 2 Answers

Solving quadratic equations using substitution

We can treat equations with a variable and the square root of a variable as “hidden” quadratic equations.

Worked Example 9 Use the substitution x = u2 to solve the equation

We should always check solutions, as some solutions may not be valid (why do you think this is?)

Worked Example 10 Solve the equation

Using graphs to solve cubic inequalities

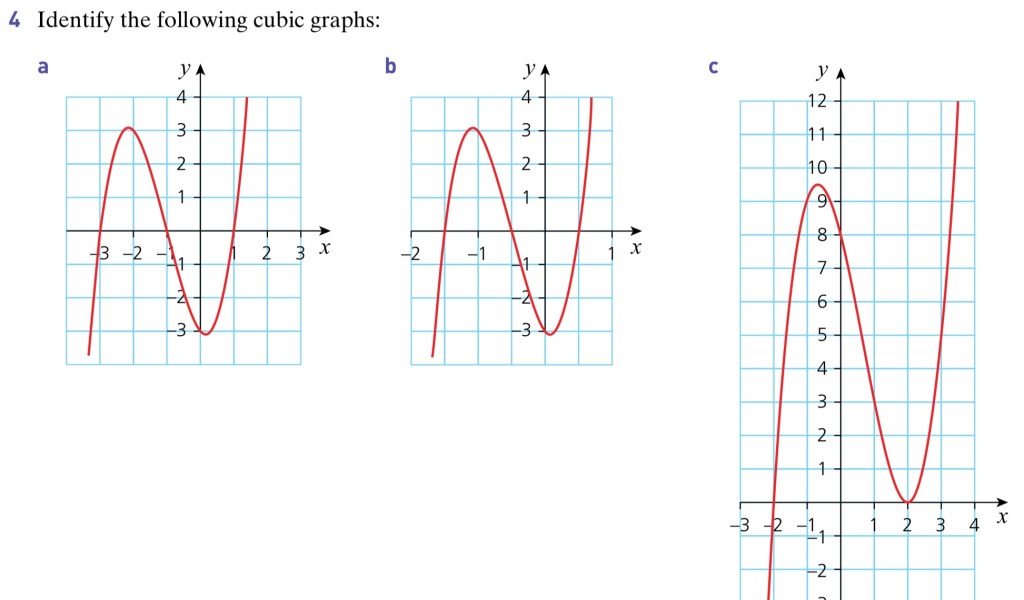
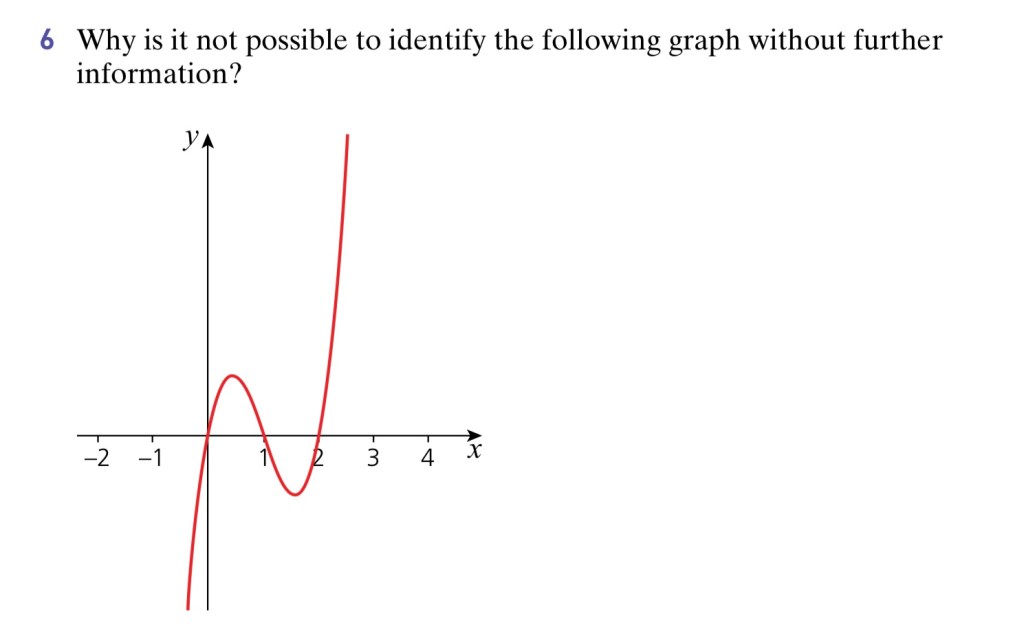
We should already be familiar with the basic shape of a cubic equation

Worked Example 11 a.) Sketch the graph of y = 3(x+2)(x-1)(x-7). Identify the points where the curve cuts the axes;  b.) Sketch the graph of y = |3(x+2)(x-1)(x-7)|.

Worked Example 12 Solve the inequality 3(x+2)(x-1)(x-7) ≤ -100 graphically.

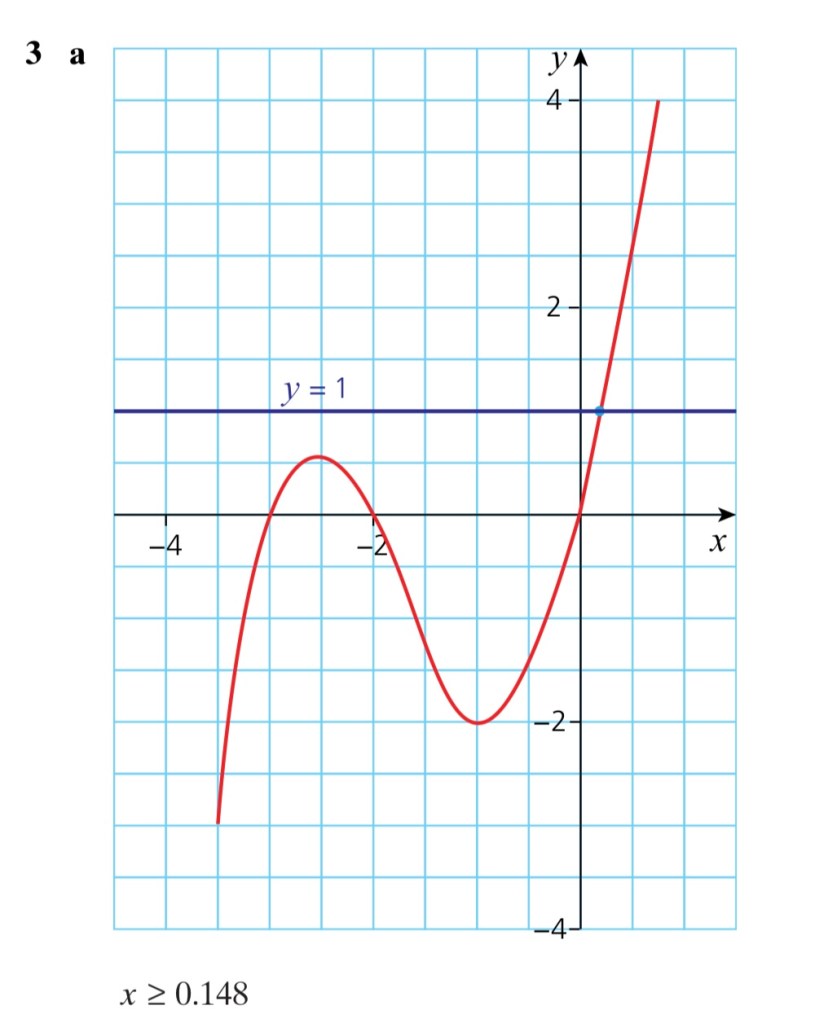
Exercise 3

Answers