Any diameter of a circle is a line of symmetry (i.e. it has infinitely many).

A circle has rotational symmetry around its centre.

Due to these two facts we can deduce the following:

• The perpendicular bisector of any chord passes through the centre of the circle;
• Equal length chords are an equal perpendicular distance from the centre (the converse is also true);
• Two tangents drawn to a circle from the same point outside the circle are equal in length.

Worked Example 1

Chord AB is drawn in a circle with a radius of 7cm. If the chord is 3cm from the centre of the circle, then find the length of the chord correct to 2 decimal places.

Worked Example 2

O is the centre of a circle with radius 11cm. AB and CD are chords, with AB = 14cm. If OX = OY, then find the length of OY correct two 2 decimal places.

Worked Example 3

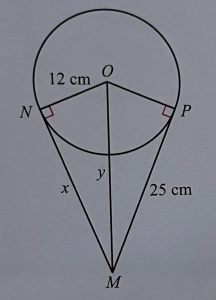
Find the lengths of x and y in this diagram correct to 2 decimal places.

Worked Example 4

Find the sizes of angles x and y in the diagram above.

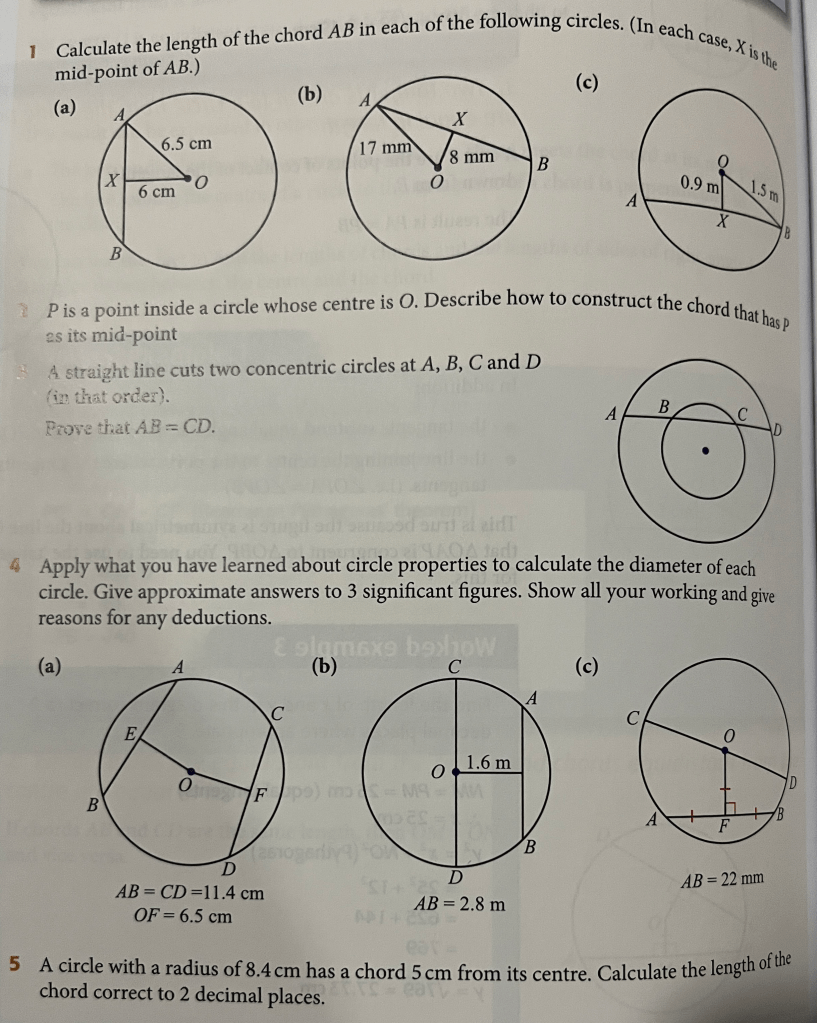
Exercise

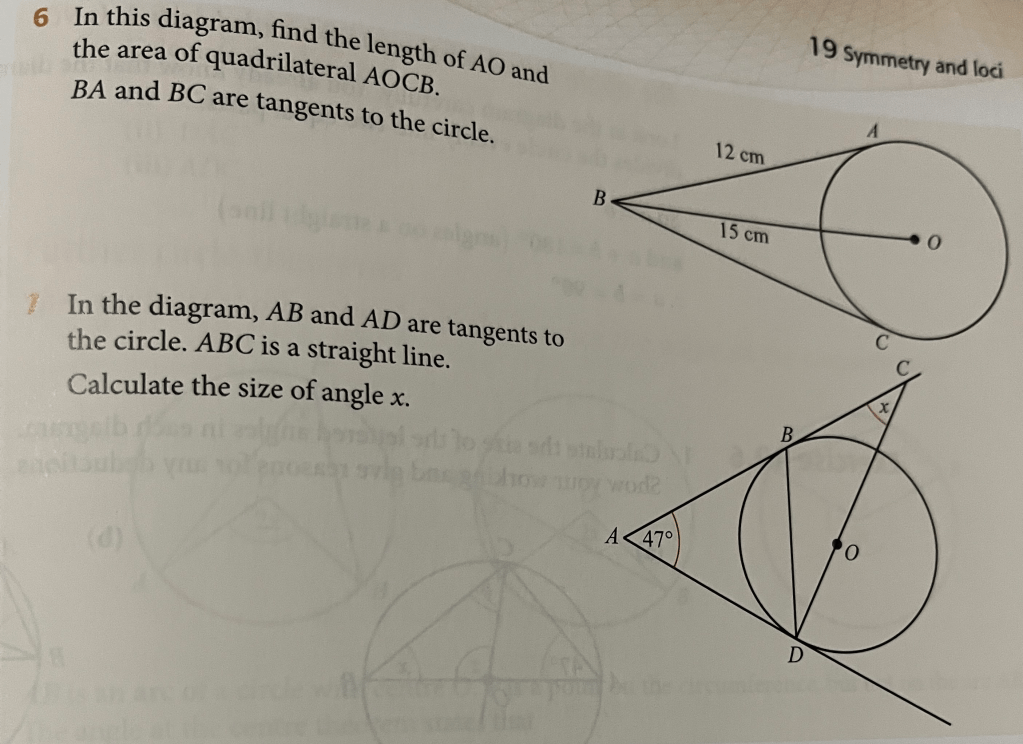
Answers